题目内容
(本小题满分12分)
已知函数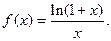
(1)确定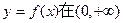 上的单调性;
上的单调性;
(2)设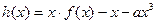 在(0,2)上有极值,求
在(0,2)上有极值,求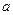 的取值范围。
的取值范围。
已知函数
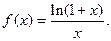
(1)确定
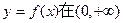 上的单调性;
上的单调性;(2)设
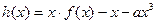 在(0,2)上有极值,求
在(0,2)上有极值,求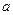 的取值范围。
的取值范围。(1)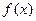 在(0,+∞)上单调递减(2)
在(0,+∞)上单调递减(2)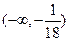
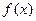 在(0,+∞)上单调递减(2)
在(0,+∞)上单调递减(2)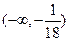
(1)由已知函数求导得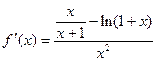 2分
2分
设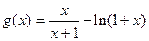 ,
,
则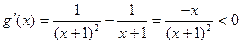 4分
4分
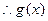 在(0,+∞)上递减,
在(0,+∞)上递减,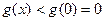 ,
,
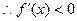 ,
,
因此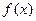 在(0,+∞)上单调递减 6分
在(0,+∞)上单调递减 6分
(2)由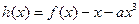 可得:
可得:
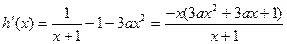 7分
7分
若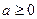 ,任给
,任给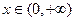 ,
,
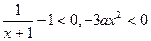
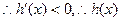 在(0,2)上单调递减,
在(0,2)上单调递减,
则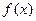 在(0,2)无极值 9分
在(0,2)无极值 9分
若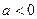 ,
,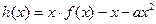 在(0,2)上有极值的充要条件是
在(0,2)上有极值的充要条件是
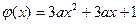 在(0,2)上有零点 11分
在(0,2)上有零点 11分
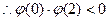 ,解得
,解得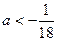
综上,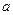 的取值范围是
的取值范围是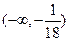 12分
12分
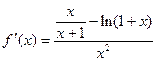 2分
2分设
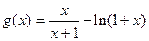 ,
,则
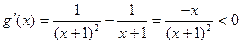 4分
4分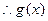 在(0,+∞)上递减,
在(0,+∞)上递减,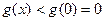 ,
,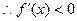 ,
,因此
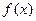 在(0,+∞)上单调递减 6分
在(0,+∞)上单调递减 6分(2)由
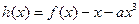 可得:
可得: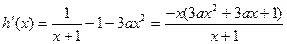 7分
7分若
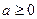 ,任给
,任给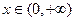 ,
,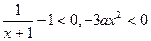
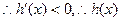 在(0,2)上单调递减,
在(0,2)上单调递减,则
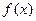 在(0,2)无极值 9分
在(0,2)无极值 9分若
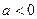 ,
,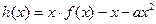 在(0,2)上有极值的充要条件是
在(0,2)上有极值的充要条件是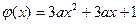 在(0,2)上有零点 11分
在(0,2)上有零点 11分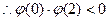 ,解得
,解得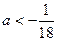
综上,
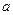 的取值范围是
的取值范围是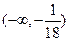 12分
12分
练习册系列答案
相关题目
 ,函数
,函数 ,
, .
. 的单调性
的单调性 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根. 函数
函数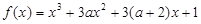 有极值;命题
有极值;命题 函数
函数 且
且 恒成立.若
恒成立.若 为真命题,
为真命题, 为真命题,则
为真命题,则 的取值范围是
的取值范围是




 =
= 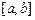 上的函数
上的函数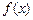 ,给出下列命题:(1)若
,给出下列命题:(1)若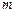 ,极小值为
,极小值为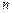 ,那么
,那么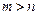 ;(3)若
;(3)若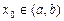 ,在
,在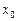 左侧附近
左侧附近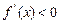 ,且
,且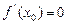 ,则
,则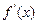 在
在 当
当 时取得极大值。当
时取得极大值。当 时取得极小值,则
时取得极小值,则 的取值范围是( )
的取值范围是( )



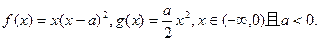
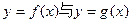 的图象的交点A的坐标;
的图象的交点A的坐标;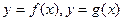 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为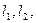 是否存在这样的实数a,使得
是否存在这样的实数a,使得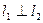 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。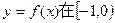 上最小值为F(a),求
上最小值为F(a),求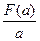 的最小值。
的最小值。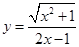 的导数是 ( )
的导数是 ( )



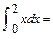 ____________
____________