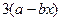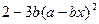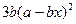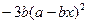题目内容
设 ,函数
,函数 ,
, .
.
(I)试讨论函数 的单调性
的单调性
(II)设 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根.
 ,函数
,函数 ,
, .
.(I)试讨论函数
 的单调性
的单调性(II)设
 ,求证:
,求证: 有三个不同的实根.
有三个不同的实根.当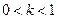 时,函数
时,函数 在
在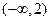 上递减,在
上递减,在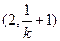 上递增,在
上递增,在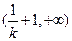 上递减;
上递减;
当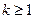 时,函数
时,函数 在
在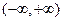 上是减函数;
上是减函数;
当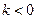 时,函数
时,函数 在
在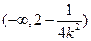 上递增,在
上递增,在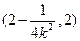 上递减,在
上递减,在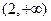 上递增.
上递增.
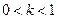 时,函数
时,函数 在
在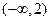 上递减,在
上递减,在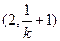 上递增,在
上递增,在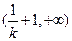 上递减;
上递减;当
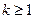 时,函数
时,函数 在
在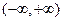 上是减函数;
上是减函数;当
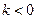 时,函数
时,函数 在
在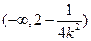 上递增,在
上递增,在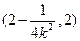 上递减,在
上递减,在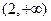 上递增.
上递增.解:(Ⅰ)∵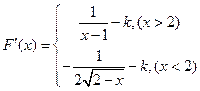 . ……………2分
. ……………2分
∴当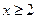 时,方程
时,方程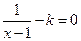 的解为:
的解为: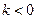 或
或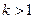 时无解,
时无解,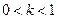 时为
时为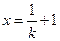 ,
,
当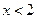 时,方程
时,方程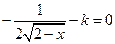 的解为:
的解为: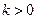 时无解,
时无解,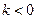 时为
时为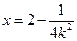 .
.
∴当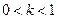 时,函数
时,函数 在
在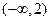 上递减,在
上递减,在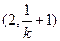 上递增,在
上递增,在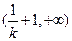 上递减;
上递减;
当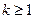 时,函数
时,函数 在
在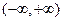 上是减函数;
上是减函数;
当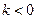 时,函数
时,函数 在
在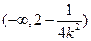 上递增,在
上递增,在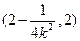 上递减,在
上递减,在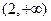 上递增. ……………7分
上递增. ……………7分
(Ⅱ)∵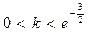 ,由(Ⅰ)可知,
,由(Ⅰ)可知, 的取值随着x的变化如下:
的取值随着x的变化如下:

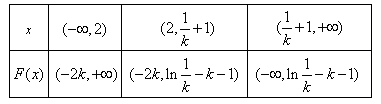
∴当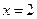 时,
时, 极小值为
极小值为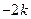 ,
,
当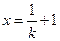 ,
, 极大值为
极大值为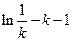 . ……………10分
. ……………10分
∵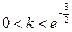 ,∴
,∴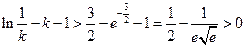 ,
,
∴ 极小
极小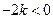 ,
, 极大值为
极大值为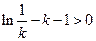 ,
,
因此,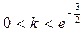 时,方程
时,方程 一定有三个不同的实根.…………12分
一定有三个不同的实根.…………12分
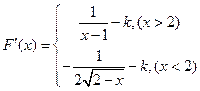 . ……………2分
. ……………2分∴当
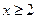 时,方程
时,方程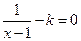 的解为:
的解为: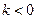 或
或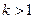 时无解,
时无解,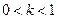 时为
时为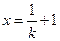 ,
,当
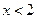 时,方程
时,方程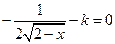 的解为:
的解为: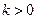 时无解,
时无解,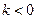 时为
时为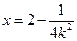 .
.∴当
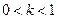 时,函数
时,函数 在
在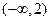 上递减,在
上递减,在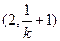 上递增,在
上递增,在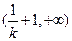 上递减;
上递减;当
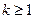 时,函数
时,函数 在
在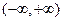 上是减函数;
上是减函数;当
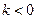 时,函数
时,函数 在
在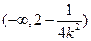 上递增,在
上递增,在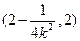 上递减,在
上递减,在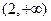 上递增. ……………7分
上递增. ……………7分(Ⅱ)∵
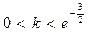 ,由(Ⅰ)可知,
,由(Ⅰ)可知, 的取值随着x的变化如下:
的取值随着x的变化如下:
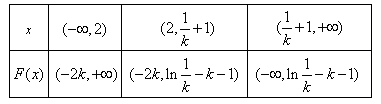
∴当
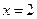 时,
时, 极小值为
极小值为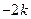 ,
,当
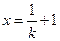 ,
, 极大值为
极大值为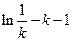 . ……………10分
. ……………10分∵
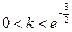 ,∴
,∴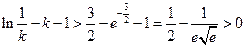 ,
,∴
 极小
极小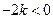 ,
, 极大值为
极大值为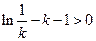 ,
,因此,
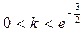 时,方程
时,方程 一定有三个不同的实根.…………12分
一定有三个不同的实根.…………12分
练习册系列答案
相关题目
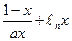 在[1,+∞
在[1,+∞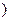 上为增函数.
上为增函数. 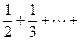
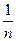
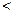
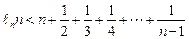 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 ) .
.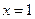 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求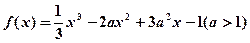 。
。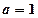 时,求函数
时,求函数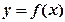 的单调增区间;
的单调增区间;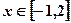 , 恒有
, 恒有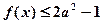 ,求
,求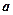 的取值范围。
的取值范围。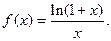
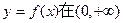 上的单调性;
上的单调性;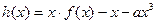 在(0,2)上有极值,求
在(0,2)上有极值,求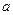 的取值范围。
的取值范围。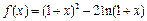 .
.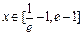 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;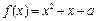 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围. ,则
,则 ( )
( )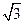

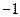

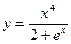 ,那么
,那么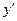 =( )
=( )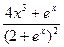
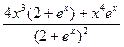

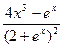
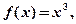 则
则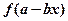 的导数是( )
的导数是( )