题目内容

19．如图，在正方体ABCD-A1B1C1D1中，直线B1B与平面A1C1D所成角的余弦值为$\frac{\sqrt{6}}{3}$．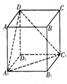
 

分析 由题意，直线B1B与平面A1C1D所成角等于直线D1D与平面A1C1D所成角α，利用等体积法求出D1到平面A1C1D的距离，即可求出直线B1B与平面A1C1D所成角的余弦值．

解答 解：由题意，直线B1B与平面A1C1D所成角等于直线D1D与平面A1C1D所成角α．
设正方体的棱长为1，D1到平面A1C1D的距离为h，则由等体积可得$\frac{1}{3}×\frac{\sqrt{3}}{4}×2×h$=$\frac{1}{3}×\frac{1}{2}×1×1×1$，
∴h=$\frac{\sqrt{3}}{3}$，
∴sinα=$\frac{\sqrt{3}}{3}$，
∴cosα=$\frac{\sqrt{6}}{3}$．
故答案为：$\frac{\sqrt{6}}{3}$．

点评 本题考查直线B1B与平面A1C1D所成角的余弦值，考查学生的计算能力，求出D1到平面A1C1D的距离是关键．

练习册系列答案
相关题目
19．已知向量$\overrightarrow m$=$（{cosx，cos（{x+\frac{π}{6}}）}），\overrightarrow n$=$（{\sqrt{3}sinx$+cosx，2sinx}），且满足f（x）=$\overrightarrow m•\overrightarrow n$．
（Ⅰ）求函数f（x）的对称轴方程；
（Ⅱ）将函数f（x）的图象向右平移$\frac{π}{6}$个单位得到g（x）的图象，当x∈[0，π]时，求函数g（x）的单调递增区间．
20．如图，三棱柱 ABC-A1B1C1 中，AA1⊥平面 A1B1C1，AB=AC=AA1=2，AB⊥AC，D 为 AC 中点，点 E 在棱 CC1C上，且 AE⊥平面 A1B1D．
（Ⅰ）求 CE 的长；
（Ⅱ）求三棱锥 E-A1BD 的体积．
7．已知点P（1，3），Q（1，2）．设过点P的动直线与抛物线y=x2交于A，B两点，直线AQ，BQ与该抛物线的另一交点分别为C，D．记直线AB，CD的斜率分
别为k1，k2．
（Ⅰ）当k1=0时，求弦AB的长；
（Ⅱ）当k1≠2时，$\frac{{k}_{2}-2}{{k}_{1}-2}$是否为定值？若是，求出该定值．
14．已知函数f（x）=alnxx+bx，（x∈（0，+∞）的图象过点（$\frac{1}{e}$，-$\frac{1}{e}$），且在点（1，f（1））处的切线与直线x+y-e=0垂直．
（1）求a，b的值．
（2）若存在x0∈[$\frac{1}{e}$，e]（e为自然对数的底数，且e=2.71828…），使得不等式f（x0）=$\frac{1}{2}$x02-$\frac{1}{2}$tx0≥-$\frac{3}{2}$成立，求实数t的取值范围；
（3）设函数f（x）的图象上从左至右依次存在三个点B（b，f（b）），C（c，f（c）），D（d，f（d）），且2c=b+d，求证：f（b）+f（d）-2f（c）＜（d-b）ln2．
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且经过点（1，$\frac{\sqrt{2}}{2}$），
（1）求椭圆C的标准方程；
（2）设Q（2，0），过点（-1，0）的直线l交C于M，N两点，△QMN的面积记为S，若对满足条件的任意直线l，不等式S≤λtan∠MQN恒成立，求λ的最小值．
11．设椭圆C的中心在原点，左，右焦点分别为F1，F2，过F1垂直x轴的直线与椭圆相交于A，B两点，|AB|=$\frac{2\sqrt{3}}{3}$，且△F2AB的周长为4$\sqrt{3}$．
（1）求椭圆C的方程；
（2）过圆D：x2+y2=4上任一点P作椭圆C的两条切线m，n，直线m，n与圆D的另一交点分别为M，N．
①证明：m⊥n；
②求△MNP面积的最大值．
8．如图是某几何体的三视图，则该几何体的体积为（　　）
A．64+32πB．64+54πC．256+64πD．256+128π
9．若存在直线l与曲线C1和曲线C2都相切，则称曲线C1和曲线C2为“相关曲线”，有下列三个命题：①有且只有两条直线l使得曲线C1：x2+y2=4和曲线C2：x2+y2-4x+2y+4=0为“相关曲线”；②曲线C1：4y2-x2=1和曲线C2：x2-4y2=1是“相关曲线”；③曲线C1：y=lnx和曲线C2：y=x2-x为“相关曲线”．其中正确命题的个数为（　　）
A．0B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网