题目内容
4.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点(1,$\frac{\sqrt{2}}{2}$),(1)求椭圆C的标准方程;
(2)设Q(2,0),过点(-1,0)的直线l交C于M,N两点,△QMN的面积记为S,若对满足条件的任意直线l,不等式S≤λtan∠MQN恒成立,求λ的最小值.
分析 (1)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点(1,$\frac{\sqrt{2}}{2}$),可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得即可得出;
(2)当MN⊥x轴时,把x=-1代入椭圆方程可得:y=±$\frac{\sqrt{2}}{2}$,|MN|=$\sqrt{2}$,可得S=$\frac{1}{2}|MN|•|QF|$.由tan∠MQF=$\frac{|MF|}{|QF|}$=$\frac{\sqrt{2}}{6}$,可得tan∠MQN=tan2∠MQF=$\frac{2tan∠MQF}{1-ta{n}^{2}∠MQF}$,代入S≤λtan∠MQN恒成立,解得$λ≥\frac{17}{4}$.
当MN与x轴不垂直时,由S≤λtan∠MQN恒成立,可得$\frac{1}{2}|\overrightarrow{QM}||\overrightarrow{QN}|sin∠MQN$$≤λ•\frac{sin∠MQN}{cos∠MQN}$,化为$λ≥\frac{1}{2}\overrightarrow{QM}•\overrightarrow{QN}$.设M(x1,y1),N(x2,y2).可得λ≥$\frac{1}{2}$[(x1-2)(x2-2)+y1y2]=$\frac{1}{2}[{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4+{y}_{1}{y}_{2}]$.可设直线l的方程为:y=k(x+1),与椭圆方程联立化为(1+2k2)x2+4k2x+2k2-2=0,利用根与系数的关系可得:$λ≥\frac{1}{2}$$[(1+{k}^{2}){x}_{1}{x}_{2}+({k}^{2}-2)({x}_{1}+{x}_{2})+{k}^{2}+4]$,即可得出.
解答 解:(1)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点(1,$\frac{\sqrt{2}}{2}$),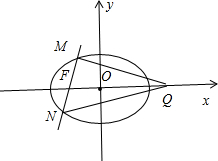
可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=1,b=c=1.
∴椭圆C的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)当MN⊥x轴时,把x=-1代入椭圆方程可得:y=±$\frac{\sqrt{2}}{2}$,|MN|=$\sqrt{2}$,
∴S=$\frac{1}{2}|MN|•|QF|$=$\frac{1}{2}×\sqrt{2}×3$=$\frac{3\sqrt{2}}{2}$.
∵tan∠MQF=$\frac{|MF|}{|QF|}$=$\frac{\sqrt{2}}{6}$,∴tan∠MQN=tan2∠MQF=$\frac{2tan∠MQF}{1-ta{n}^{2}∠MQF}$=$\frac{6\sqrt{2}}{17}$,
∵S≤λtan∠MQN恒成立,
∴$\frac{3\sqrt{2}}{2}≤λ•\frac{6\sqrt{2}}{17}$,
解得$λ≥\frac{17}{4}$.
当MN与x轴不垂直时,∵S≤λtan∠MQN恒成立,∴$\frac{1}{2}|\overrightarrow{QM}||\overrightarrow{QN}|sin∠MQN$$≤λ•\frac{sin∠MQN}{cos∠MQN}$,
∴$λ≥\frac{1}{2}\overrightarrow{QM}•\overrightarrow{QN}$.
设M(x1,y1),N(x2,y2).$\overrightarrow{QM}$(x1-2,y1),$\overrightarrow{QN}$=(x2-2,y2).
则λ≥$\frac{1}{2}$[(x1-2)(x2-2)+y1y2]=$\frac{1}{2}[{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4+{y}_{1}{y}_{2}]$.
∵MN与x轴不垂直时,可设直线l的方程为:y=k(x+1),
联立$\left\{\begin{array}{l}{y=k(x+1)}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,化为(1+2k2)x2+4k2x+2k2-2=0,
∴x1+x2=$\frac{-4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$.
∴y1y2=k2(x1+1)(x2+1)=${k}^{2}{x}_{1}{x}_{2}+{k}^{2}({x}_{1}+{x}_{2})+{k}^{2}$,
∴$λ≥\frac{1}{2}$$[(1+{k}^{2}){x}_{1}{x}_{2}+({k}^{2}-2)({x}_{1}+{x}_{2})+{k}^{2}+4]$=$\frac{1}{2}[\frac{(2{k}^{2}-2)(1+{k}^{2})}{1+2{k}^{2}}-\frac{4{k}^{2}({k}^{2}-2)}{1+2{k}^{2}}+{k}^{2}+4]$=$\frac{1}{2}×\frac{17{k}^{2}+2}{1+2{k}^{2}}$=$\frac{17}{4}$-$\frac{13}{4(2{k}^{2}+1)}$.
∴$λ>\frac{17}{4}$.
综上可得:$λ≥\frac{17}{4}$.
∴λ的最小值为$\frac{17}{4}$.
点评 本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数的关系、向量数量积运算性质、三角形面积计算公式、不等式的性质,考查了恒成立问题的等价转化方法、推理能力与计算能力,属于难题.

 如图,在正方体ABCD-A1B1C1D1中,O1为底面的中心,则O1A与上底面A1B1C1D1所成角的正切值是( )
如图,在正方体ABCD-A1B1C1D1中,O1为底面的中心,则O1A与上底面A1B1C1D1所成角的正切值是( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |