题目内容
8．如图是某几何体的三视图，则该几何体的体积为（ ）
| A． | 64+32π | B． | 64+54π | C． | 256+64π | D． | 256+128π |
分析 根据几何体的三视图，得出该几何体是长方体与圆柱体的组合体，由此求出它的体积．
解答 解：根据几何体的三视图，得；
该几何体是长和宽为8，高为4的长方体，
与底面直径为8，高为4的圆柱体的组合体，
如图所示；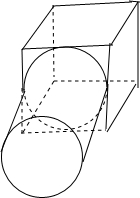
∴该几何体的体积为
V正方体+V圆柱体=8×8×4+π×42×4=256+64π．
故选：C．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键是根据三视图得出几何体的结构特征是什么，属于基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．设函数f（x）=exsinx-cosx，g（x）=xcosx-$\sqrt{2}$ex（其中e是自然对数的底数），?x1∈[0，$\frac{π}{2}$]，?x2∈[0，$\frac{π}{2}$]，使得不等式f（x1）+g（x2）≥m成立，则实数m的范围（ ）
| A． | （-∞，-1-$\sqrt{2}$] | B． | （-∞，${e}^{\frac{π}{2}}$-$\sqrt{2}$] | C． | （-∞，-1-$\sqrt{2}$${e}^{\frac{π}{2}}$] | D． | （-∞，（-1-$\sqrt{2}$）${e}^{\frac{π}{2}}$] |
3．已知P、Q两点的极坐标分别为（4，$\frac{2π}{3}$）、（2，$\frac{π}{3}$），在直角坐标系中，下列各点在线段PQ的垂直平分线上的为（ ）
| A． | （0，2$\sqrt{3}$） | B． | （-$\frac{1}{2}$，2$\sqrt{3}$） | C． | （0，-2$\sqrt{3}$） | D． | （-$\frac{1}{2}$，-2$\sqrt{3}$） |
18．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x+a，x＜\frac{1}{2}}\\{{4}^{x}-3，x≥\frac{1}{2}}\end{array}\right.$的最小值为-1，则实数a的取值范围是（ ）
| A． | a≥-2 | B． | a＞-2 | C． | a≥-$\frac{1}{4}$ | D． | a＞-$\frac{1}{4}$ |