题目内容
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由长轴长可得![]() 值,公共弦长恰为圆
值,公共弦长恰为圆![]() 直径,可知椭圆经过点
直径,可知椭圆经过点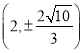 ,利用待定系数法可得椭圆
,利用待定系数法可得椭圆![]() 方程;(2)可令直线
方程;(2)可令直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
, ![]() 的中点为
的中点为![]() ,将直线方程与椭圆方程联立,消去
,将直线方程与椭圆方程联立,消去![]() ,利用根与系数的关系可得
,利用根与系数的关系可得![]() ,由等腰三角形中
,由等腰三角形中![]() ,可得
,可得![]() ,得出
,得出![]() 中
中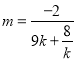 .由此可得
.由此可得![]() 点的横坐标
点的横坐标![]() 的范围.
的范围.
试题解析:(1)由题意可得![]() ,所以
,所以![]() .由椭圆
.由椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() ,恰为圆
,恰为圆![]() 的直径,可得椭圆
的直径,可得椭圆![]() 经过点
经过点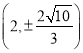 ,所以
,所以![]() ,解得
,解得![]() .所以椭圆
.所以椭圆![]() 的方程为
的方程为![]() .
.
(2)直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
, ![]() 的中点为
的中点为![]() .假设存在点
.假设存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,则
为底边的等腰三角形,则![]() .由
.由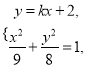 得
得![]() ,故
,故![]() ,所以
,所以![]() ,
, ![]() .因为
.因为![]() ,所以
,所以![]() ,即
,即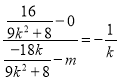 ,所以
,所以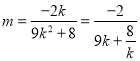 .当
.当![]() 时,
时, ![]() ,所以
,所以![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() .
.
综上所述,在![]() 轴上存在满足题目条件的点
轴上存在满足题目条件的点![]() ,且点
,且点![]() 的横坐标的取值范围为
的横坐标的取值范围为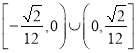 .
.

【题目】下表给出![]() 三种食物的维生素含量及其成本:
三种食物的维生素含量及其成本:
|
|
| |
维生素A(单位/千克) | 4000 | 5000 | 300 |
维生素B(单位/千克) | 700 | 100 | 300 |
成本(元/千克) | 6 | 4 | 3 |
现欲将三种食物混合成本100千克的混合食品,要求至少含35000单位维生素A,40000单位维生素B,采用何种配比成本最小?
【题目】我校举行的 “青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ▓ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |
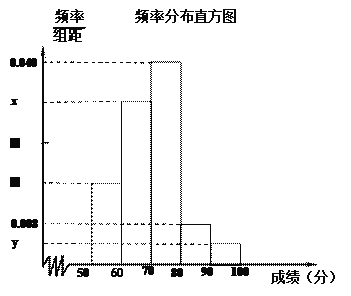
(1)求出![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的众数、中位数和平均数。