题目内容
【题目】已知双曲线 
的左、右焦点分别为F1、F2 ， P为C的右支上一点，且|PF2|=|F1F2|，则 
等于（ ）
A.24
B.48
C.50
D.56
【答案】C
【解析】解：根据双曲线方程 
， 得a2=4，b2=5，c= 
=3，所以双曲线的焦点分别为F1（﹣3，0）、F2（3，0），
设点P的坐标为（m，n），其中m＞2，则
∵点P在双曲线上，且|PF2|=|F1F2|，
∴ 
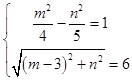，解之得m= 
，n=± 
∵ 
=（﹣3﹣m，﹣n）， 
=（3﹣m，﹣n）
∴ 
=（﹣3﹣m）（3﹣m）+（﹣n）（﹣n）=m2﹣9+n2= 
﹣9+ 
=50
故选C
设点P的坐标为（m，n），其中m＞2，根据点P在双曲线上且|PF2|=|F1F2|，建立关于m、n的方程组，解之得m、n的值，从而得到向量 、 的坐标，利用向量数量积的坐标公式，可算出 的值．
练习册系列答案
相关题目
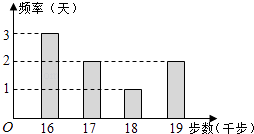
【题目】小王为了锻炼身体，每天坚持“健步走”，并用计步器进行统计．小王最近8天“健步走”步数的频数分布直方图（图1）及相应的消耗能量数据表（表1）如下：
健步走步数（前步） | 16 | 17 | 18 | 19 |
消耗能量（卡路里） | 400 | 440 | 480 | 520 |
（Ⅰ）求小王这8天“健步走”步数的平均数；
（Ⅱ）从步数为17千步，18千步，19千步的几天中任选2天，求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率．