题目内容
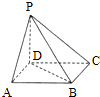
【题目】如图,正方形BCDE的边长为a,已知AB= ![]() BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: 
① AB与DE所成角的正切值是 ![]() ;
;
②AB∥CE
③VB﹣ACE体积是 ![]() a3;
a3;
④平面ABC⊥平面ADC.
其中正确的有 . (填写你认为正确的序号)
【答案】①③④
【解析】解:作出折叠后的几何体直观图如图所示: ∵AB= ![]() a,BE=a,∴AE=
a,BE=a,∴AE= ![]() a.
a.
∴AD= ![]() .∴AC=
.∴AC= ![]() .
.
在△ABC中,cos∠ABC= ![]() =
= ![]() =
= ![]() .
.
∴sin∠ABC= ![]() =
= ![]() .
.
∴tan∠ABC= ![]() =
= ![]() .
.
∵BC∥DE,∴∠ABC是异面直线AB,DE所成的角,故①正确.
连结BD,CE,则CE⊥BD,
又AD⊥平面BCDE,CE平面BCDE,
∴CE⊥AD,又BD∩AD=D,BD平面ABD,AD平面ABD,
∴CE⊥平面ABD,又AB平面ABD,
∴CE⊥AB.故②错误.
三棱锥B﹣ACE的体积V= ![]() =
= ![]() =
= ![]() ,故③正确.
,故③正确.
∵AD⊥平面BCDE,BC平面BCDE,
∴BC⊥AD,又BC⊥CD,
∴BC⊥平面ACD,∵BC平面ABC,
∴平面ABC⊥平面ACD.
所以答案是①③④.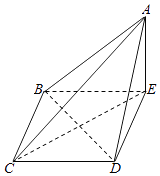

练习册系列答案
相关题目