题目内容
(本小题共14分)
已知数列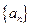 中,
中,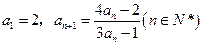 ,设
,设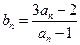 .
.
(Ⅰ)试写出数列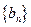 的前三项;
的前三项;
(Ⅱ)求证:数列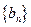 是等比数列,并求数列
是等比数列,并求数列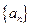 的通项公式
的通项公式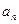 ;
;
(Ⅲ)设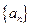 的前
的前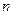 项和为
项和为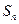 ,求证:
,求证: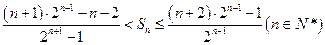 .
.
已知数列
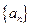 中,
中,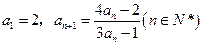 ,设
,设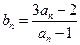 .
.(Ⅰ)试写出数列
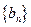 的前三项;
的前三项;(Ⅱ)求证:数列
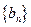 是等比数列,并求数列
是等比数列,并求数列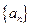 的通项公式
的通项公式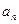 ;
;(Ⅲ)设
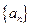 的前
的前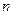 项和为
项和为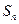 ,求证:
,求证: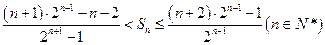 .
.(1)
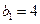 ,
,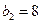 ,
,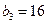
(2)
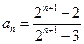
(3)略
解:(Ⅰ)由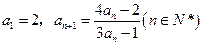 ,得
,得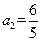 ,
,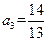 .
.
由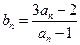 ,可得
,可得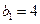 ,
,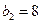 ,
,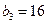 . -------------------3分
. -------------------3分
(Ⅱ)证明:因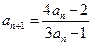 ,故
,故
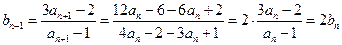 . ---------------------5分
. ---------------------5分
显然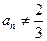 ,因此数列
,因此数列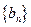 是以
是以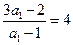 为首项,以2为公比的等比数列,
为首项,以2为公比的等比数列,
即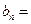
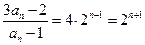 . --------------------7分
. --------------------7分
解得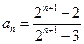 . ---------------------8分
. ---------------------8分
(Ⅲ)因为
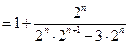
 ,
,
所以
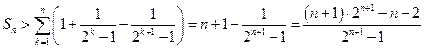 ;
;
---------------------11分
又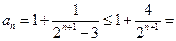
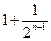 (当且仅当
(当且仅当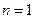 时取等号),
时取等号),
故
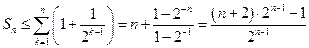 .
.
综上可得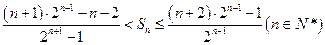 .--------------------14分
.--------------------14分
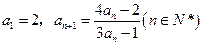 ,得
,得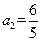 ,
,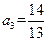 .
.由
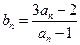 ,可得
,可得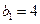 ,
,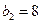 ,
,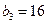 . -------------------3分
. -------------------3分(Ⅱ)证明:因
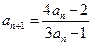 ,故
,故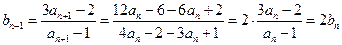 . ---------------------5分
. ---------------------5分显然
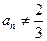 ,因此数列
,因此数列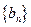 是以
是以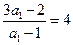 为首项,以2为公比的等比数列,
为首项,以2为公比的等比数列,即
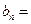
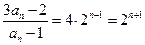 . --------------------7分
. --------------------7分解得
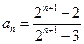 . ---------------------8分
. ---------------------8分(Ⅲ)因为

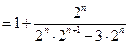
 ,
,所以
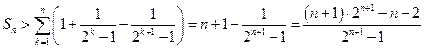 ;
;---------------------11分
又
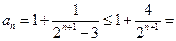
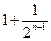 (当且仅当
(当且仅当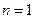 时取等号),
时取等号),故
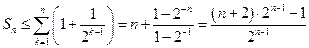 .
. 综上可得
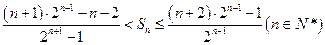 .--------------------14分
.--------------------14分
练习册系列答案
相关题目
 求数列满足
求数列满足 ,
, ,则
,则 是递增数列,则实数
是递增数列,则实数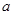 取值范围是( )
取值范围是( )
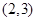

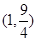
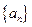 的前
的前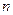 项和为
项和为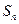 ,点
,点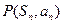 在直线
在直线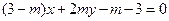 上,
上,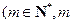 为常数,
为常数,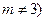 .
.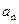 ;
;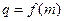 ,数列
,数列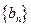 满足
满足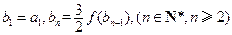 ,求证:
,求证: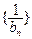 为等差数列,并求
为等差数列,并求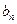 ;
;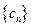 满足
满足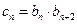 ,
,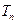 为数列
为数列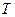 满足
满足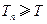 ,
,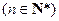 ,求
,求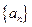 的前
的前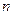 项和
项和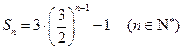 ,数列
,数列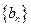 满足:
满足: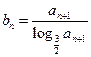
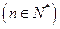 .
. 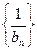 的前n项和
的前n项和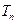 ;
; 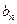 的最小值.
的最小值.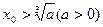 ,由递推公式
,由递推公式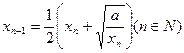 得到数列
得到数列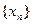 ,对于任意的
,对于任意的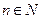 ,都有
,都有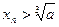 ,用数列
,用数列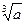 的近似值。
的近似值。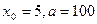 ,计算
,计算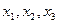 的值(精确到0.01);归纳出
的值(精确到0.01);归纳出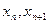 的大小关系;
的大小关系;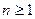 时,证明:
时,证明: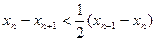 ;
;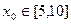 时,用数列
时,用数列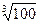 的近似值,要求
的近似值,要求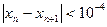 ,请你估计n,并说明理由
,请你估计n,并说明理由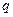 ,每列上的数从上到下都成等差数列,正数
,每列上的数从上到下都成等差数列,正数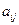 表示位于第
表示位于第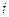 行第
行第 列的数,其中
列的数,其中
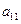
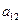

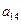







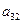
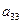

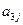



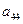


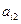


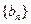 满足
满足 的前
的前 项和为
项和为 ,
, 的大小,并说明理由。
的大小,并说明理由。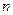 行
行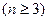 从左向右的第
从左向右的第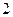 个数为
个数为 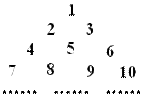
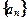 满足
满足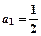 ,
,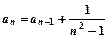 (
( ),则
),则