题目内容
当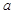 为任意实数时,直线
为任意实数时,直线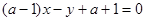 恒过定点
恒过定点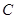 ,则以
,则以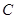 为圆心,
为圆心,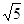 为半径的圆的方程是_____________.
为半径的圆的方程是_____________.
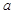 为任意实数时,直线
为任意实数时,直线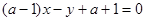 恒过定点
恒过定点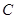 ,则以
,则以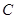 为圆心,
为圆心,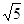 为半径的圆的方程是_____________.
为半径的圆的方程是_____________.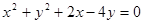
因为直线(a-1)x-y+a+1=0,即 a(x+1)+(-x-y+1)=0,定点C的坐标是方程组
X+1=0,-x-y+1=0的解∴定点C的坐标是(-1,2),再由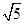 为半径可得圆的方程是 (x+1)2+(y-2)2=5,故答案为 x2+y2+2x-4y=0
为半径可得圆的方程是 (x+1)2+(y-2)2=5,故答案为 x2+y2+2x-4y=0
X+1=0,-x-y+1=0的解∴定点C的坐标是(-1,2),再由
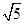 为半径可得圆的方程是 (x+1)2+(y-2)2=5,故答案为 x2+y2+2x-4y=0
为半径可得圆的方程是 (x+1)2+(y-2)2=5,故答案为 x2+y2+2x-4y=0
练习册系列答案
相关题目
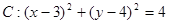 和直线
和直线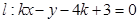
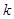 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;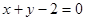 上的圆的方程是 .
上的圆的方程是 .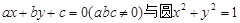 相离,若
相离,若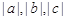 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________. 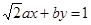 与圆
与圆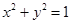 相交于
相交于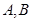 两点(其中
两点(其中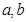 是实数),且
是实数),且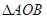 是直角三角形(
是直角三角形(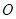 是坐标原点),则点
是坐标原点),则点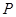
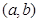 与点
与点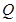
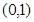 之间距离的最大值为 ( )
之间距离的最大值为 ( )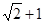
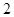

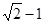
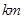 的圆形村落,
的圆形村落,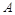 、
、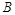 两人同时从村落中心出发。
两人同时从村落中心出发。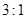 ,且后来
,且后来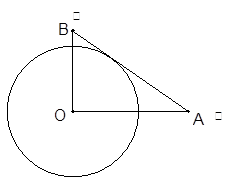
 ,斜率
,斜率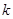 的直线
的直线 与椭圆相交于点
与椭圆相交于点 ,点
,点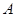 是线段
是线段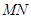 的中点,直线
的中点,直线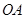 (
(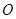 为坐标原点)的斜率是
为坐标原点)的斜率是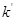 ,那么
,那么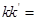
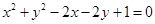 上的点到直线
上的点到直线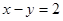 的距离的最大值是
的距离的最大值是 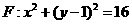 上运动,
上运动,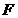 为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹
为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹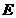 的方程;若曲线
的方程;若曲线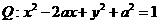 被轨迹
被轨迹 的最小值.(2)已知
的最小值.(2)已知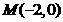 、
、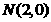 ,动点
,动点 在圆
在圆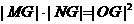 ,求
,求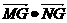 的取值范围.
的取值范围.