题目内容
(本题满分12分) 已知圆 的圆心
的圆心 在
在 轴上,半径为1,直线
轴上,半径为1,直线 ,被圆
,被圆 所截的弦长为
所截的弦长为 ,且圆心
,且圆心 在直线
在直线 的下方.
的下方.
(I)求圆 的方程;
的方程;
(II)设 ,若圆
,若圆 是
是 的内切圆,求△
的内切圆,求△ 的面积
的面积
 的最大值和最小值.
的最大值和最小值.
 的圆心
的圆心 在
在 轴上,半径为1,直线
轴上,半径为1,直线 ,被圆
,被圆 所截的弦长为
所截的弦长为 ,且圆心
,且圆心 在直线
在直线 的下方.
的下方.(I)求圆
 的方程;
的方程;(II)设
 ,若圆
,若圆 是
是 的内切圆,求△
的内切圆,求△ 的面积
的面积 的最大值和最小值.
的最大值和最小值.(I)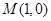 ,即圆
,即圆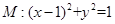 .
.
(II)S(max)=6(1 + 1/4 )=15/2 ,S(min)="6(1+" 1/8)=27/4
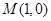 ,即圆
,即圆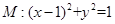 .
.(II)S(max)=6(1 + 1/4 )=15/2 ,S(min)="6(1+" 1/8)=27/4
本题是中档题,考查直线与圆的位置关系,三角形面积的最值的求法,考查计算能力.
(I)设圆心M(a,0),利用M到l:8x-6y-3=0的距离,求出M坐标,然后求圆M的方程;
(II)设A(0,t),B(0,t+6)(-5≤t≤-2),设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值和最小值.
解: ,即
,即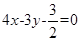 .设圆心
.设圆心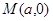 ,弦长的一半为
,弦长的一半为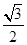 ,半径
,半径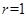 ,
,
故 到直线
到直线 的距离
的距离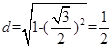 ,又
,又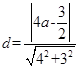 ,所以
,所以 ,解得
,解得 或
或 ,即
,即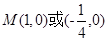 .又因为
.又因为 在
在 下方,所以
下方,所以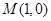 ,即圆
,即圆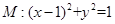 .
.
(II)设直线AC、BC的斜率分别为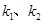 ,易知
,易知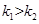 ,即
,即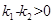 ,则
,则
直线AC的方程为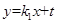 ,直线BC的方程为
,直线BC的方程为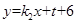 ,联立解得点C横坐标为
,联立解得点C横坐标为 ,
,
因为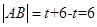 ,所以△ABC的面积
,所以△ABC的面积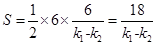 .
.
∵AC、BC与圆M相切, ∴圆心M到AC的距离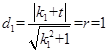 ,解得
,解得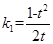 ,
,
圆心M到BC的距离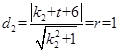 ,解得
,解得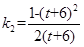 .
.
所以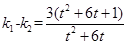 ,
, 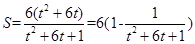
∵-5≤t≤-2 ∴-2≤t+3≤1 ∴0≤(t+3)²≤4
∴-8≤t²+6t+1= (t+3)²-8≤-4 ∴S(max)=6(1 + 1/4 )=15/2
S(min)="6(1+" 1/8)=27/4
(I)设圆心M(a,0),利用M到l:8x-6y-3=0的距离,求出M坐标,然后求圆M的方程;
(II)设A(0,t),B(0,t+6)(-5≤t≤-2),设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值和最小值.
解:
 ,即
,即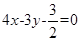 .设圆心
.设圆心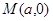 ,弦长的一半为
,弦长的一半为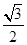 ,半径
,半径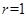 ,
,故
 到直线
到直线 的距离
的距离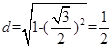 ,又
,又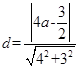 ,所以
,所以 ,解得
,解得 或
或 ,即
,即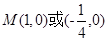 .又因为
.又因为 在
在 下方,所以
下方,所以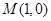 ,即圆
,即圆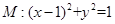 .
.(II)设直线AC、BC的斜率分别为
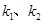 ,易知
,易知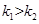 ,即
,即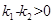 ,则
,则直线AC的方程为
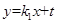 ,直线BC的方程为
,直线BC的方程为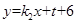 ,联立解得点C横坐标为
,联立解得点C横坐标为 ,
,因为
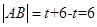 ,所以△ABC的面积
,所以△ABC的面积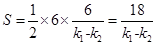 .
.∵AC、BC与圆M相切, ∴圆心M到AC的距离
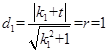 ,解得
,解得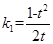 ,
,圆心M到BC的距离
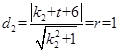 ,解得
,解得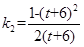 .
.所以
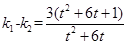 ,
, 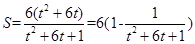
∵-5≤t≤-2 ∴-2≤t+3≤1 ∴0≤(t+3)²≤4
∴-8≤t²+6t+1= (t+3)²-8≤-4 ∴S(max)=6(1 + 1/4 )=15/2
S(min)="6(1+" 1/8)=27/4

练习册系列答案
相关题目
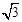 ,求直线l的方程.
,求直线l的方程.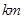 的圆形村落,
的圆形村落,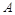 、
、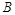 两人同时从村落中心出发。
两人同时从村落中心出发。 ,且后来
,且后来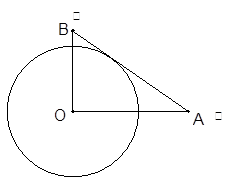
 ,斜率
,斜率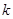 的直线
的直线 与椭圆相交于点
与椭圆相交于点 ,点
,点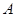 是线段
是线段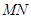 的中点,直线
的中点,直线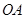 (
(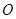 为坐标原点)的斜率是
为坐标原点)的斜率是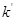 ,那么
,那么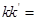
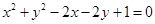 上的点到直线
上的点到直线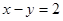 的距离的最大值是
的距离的最大值是 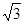 x-4的距离的最小值是 .
x-4的距离的最小值是 .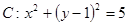 ,直线
,直线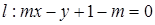
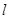 恒过定点;
恒过定点;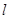 与圆交于
与圆交于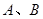 两点,若
两点,若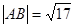 ,求直线
,求直线
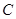 经过
经过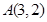 、
、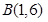 两点,且圆心在直线
两点,且圆心在直线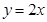 上.
上.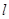 经过点
经过点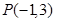 且与圆
且与圆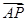 ·
·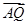 的值为______.
的值为______.