题目内容
已知p:f(x)=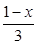 ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
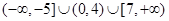 .
.
解析试题分析:由p为真命题得出a的取值范围,再由q为真命题得出a的取值范围,根据题意知,p、q一真一假,分类讨论解答.
试题解析:若|f(a)|=|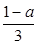 |<2成立,则-6<1-a<6,
|<2成立,则-6<1-a<6,
即当-5<a<7时p是真命题 3分
若A≠Ø,则方程x2+(a+2)x+1=0有实数根,
由Δ=(a+2)24≥0,解得a≤4,或a≥0,
即当a≤4,或a≥0时q是真命题; 6分
由于p∨q为真命题,p∧q为假命题,∴p与q一真一假,
p真q假时,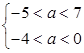 ,∴4<a<0. 8分
,∴4<a<0. 8分
p假q真时,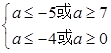 ,∴a≤5或a≥7. 10分
,∴a≤5或a≥7. 10分
故知所求a的取值范围是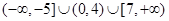 . 12分
. 12分
考点:命题及其关系、绝对值不等式的解法、一元二次方程解的情况.

练习册系列答案
相关题目
 :“方程
:“方程 表示双曲线”(
表示双曲线”(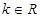 );命题
);命题 :
: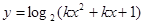 定义域为
定义域为 .若命题
.若命题 为真命题,
为真命题,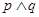 为假命题,求实数
为假命题,求实数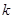 的取值范围.
的取值范围.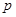 :“不等式
:“不等式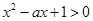 对任意
对任意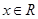 恒成立”,命题
恒成立”,命题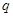 :“
:“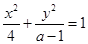 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若 为真命题,
为真命题,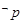 为真,求实数
为真,求实数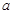 的取值范围.
的取值范围. :实数x满足
:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数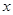 满足
满足 .
. 且
且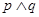 为真,求实数
为真,求实数 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数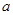 的取值范围.
的取值范围. :方程
:方程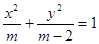 表示的曲线为椭圆;命题
表示的曲线为椭圆;命题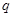 :方程
:方程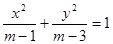 表示的曲线为双曲线;若
表示的曲线为双曲线;若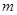 的取值范围.
的取值范围.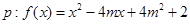 在区间
在区间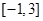 上的最小值等于2;命题
上的最小值等于2;命题 .如果“命题
.如果“命题 且
且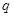 为假命题” , “命题
为假命题” , “命题 的取值范围.
的取值范围. 的定义域为R;命题q:
的定义域为R;命题q: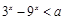 对一切的实数
对一切的实数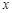 恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
恒成立,如果命题“p且q”为假命题,求实数a的取值范围. :方程
:方程 有两个不等的负实根,命题
有两个不等的负实根,命题 :方程
:方程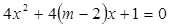 无实根.若
无实根.若 为真,
为真,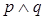 为假,求实数
为假,求实数 的取值范围.
的取值范围. 在R上是减函数;命题q:在平面直角坐标系中,点
在R上是减函数;命题q:在平面直角坐标系中,点 在直线
在直线 的左下方。若
的左下方。若 为假,
为假, 为真,求实数
为真,求实数 的取值范围
的取值范围