题目内容
已知命题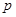 :“不等式
:“不等式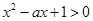 对任意
对任意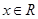 恒成立”,命题
恒成立”,命题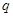 :“
:“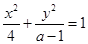 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若 为真命题,
为真命题,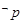 为真,求实数
为真,求实数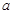 的取值范围.
的取值范围.
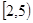
解析试题分析:由命题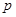 :“不等式
:“不等式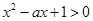 对任意
对任意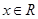 恒成立”,有判别式小于零可求得
恒成立”,有判别式小于零可求得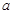 得范围;再根据命题
得范围;再根据命题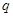 :“方程
:“方程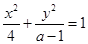 表示焦点在x轴上的椭圆”,同样可求得
表示焦点在x轴上的椭圆”,同样可求得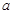 的范围.因为
的范围.因为 为真命题,
为真命题,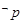 为真所以可得
为真所以可得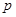 为假,所以可得
为假,所以可得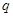 为真.从而可求出
为真.从而可求出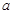 的取值范围.
的取值范围.
试题解析:因为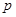 为真:
为真: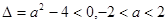 ;
; 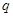 为真:
为真: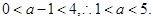 4分
4分
因为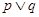 为真命题,
为真命题,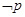 为真,所以
为真,所以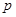 假
假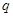 真,
真,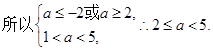 则
则 的取值范围是
的取值范围是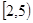 . 10分
. 10分
考点:1.二次不等式的知识.2.椭圆的性质.3.简单的逻辑关联词.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
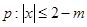 ;
;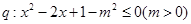 ,若
,若 是
是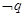 的必要非充分条件,求实数
的必要非充分条件,求实数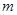 的取值范围.
的取值范围.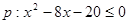 ;
; ,若
,若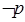 是
是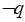 的必
的必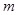 的取值范围.
的取值范围.  :实数
:实数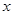 满足
满足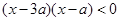 ,其中
,其中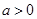 ,
,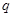 :实数
:实数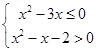 .
.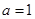 ,
,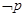 是
是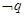 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. 方程
方程 在
在 上有解;命题
上有解;命题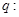 不等式
不等式 恒成立,若命题“
恒成立,若命题“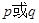 ”是假命题,求
”是假命题,求 的取值范围.
的取值范围. 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式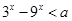 对一切实数均成立。
对一切实数均成立。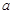 的取值范围;
的取值范围;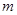 的取值组成的集合
的取值组成的集合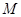 ,使当
,使当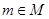 时,“
时,“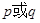 ”为真,“
”为真,“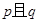 ”为假.
”为假.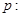 方程
方程 有两个不相等的负根;
有两个不相等的负根; 方程
方程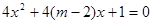 无实数根.
无实数根.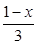 ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.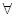 x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“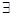 x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。