题目内容
已知命题 :方程
:方程 有两个不等的负实根,命题
有两个不等的负实根,命题 :方程
:方程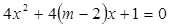 无实根.若
无实根.若 为真,
为真,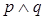 为假,求实数
为假,求实数 的取值范围.
的取值范围.
实数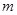 的取值范围为
的取值范围为
解析试题分析:
思路分析:根据 为真,
为真,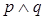 为假,确定p,q之一为真,另一为假。
为假,确定p,q之一为真,另一为假。
因此,应确定p,q为真命题时,m的范围,
然后根据 真
真 假,
假,  假
假 真,分别求得m的范围,确定它们的“并集”。
真,分别求得m的范围,确定它们的“并集”。
解:对于命题 :方程
:方程 有两个不等的负实根
有两个不等的负实根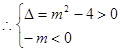 ,解得:
,解得: 3分
3分
对于命题 :方程
:方程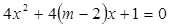 无实根
无实根 ,解得:
,解得: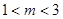 6分
6分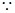
 为真,
为真,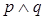 为假
为假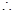
 一真一假 7分
一真一假 7分
若 真
真 假,则
假,则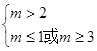 ,解得:
,解得: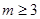 10分
10分
若 假
假 真,则
真,则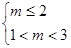 ,解得:
,解得: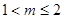 13分
13分
综上,实数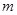 的取值范围为
的取值范围为 14分
14分
考点:复合命题真值表
点评:中档题,利用复合命题真值表,确定p,q的真假情况。通过研究时命题p,q为真命题时的m范围,达到解题目的。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 :实数
:实数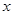 满足
满足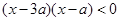 ,其中
,其中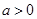 ,
,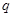 :实数
:实数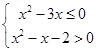 .
.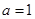 ,
,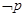 是
是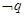 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.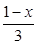 ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.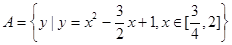 ,
,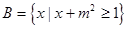 .命题
.命题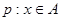 ,命题
,命题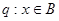 ,且命题
,且命题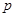 是命题
是命题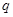 的充分条件,求实数
的充分条件,求实数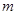 的取值范围.
的取值范围.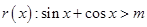 ;
; ,如果
,如果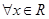 ,
,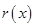 与
与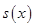 有且仅有一个是真命题,求实数
有且仅有一个是真命题,求实数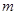 的取值范围.
的取值范围. :不等式
:不等式 的解集为R,命题
的解集为R,命题 :
: 是
是 上的增函数,若
上的增函数,若 的取值范围.
的取值范围.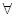 x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“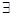 x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。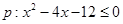 ,
,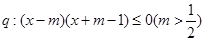 ,且
,且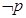 是
是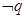 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.  ,命题
,命题 :
: 在区间
在区间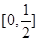 上为减函数;命题
上为减函数;命题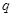 :方程
:方程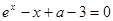 在
在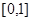 有解。若
有解。若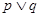 为真,
为真,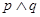 为假,求实数
为假,求实数 的取值范围。
的取值范围。