题目内容
5.定义在R上的函数f(x)满足f(x)=$\frac{f′(1)}{2}$e2x-2+x2-2f(0)x,g(x)=f($\frac{x}{2}$)-$\frac{1}{4}$x2+(1-a)x+a.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数g(x)的单调区间;
(Ⅲ) 如果s、t、r满足|s-r|≤|t-r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较$\frac{e}{x}$和ex-1+a哪个更靠近lnx,并说明理由.
分析 (Ⅰ)对f(x)求导求出f′(1)的值求出解析式.
(Ⅱ)f(x)=e2x-2x+x2,$g(x)=f(\frac{x}{2})-\frac{1}{4}{x^2}+(1-a)x+a={e^x}+\frac{1}{4}{x^2}-x-\frac{1}{4}{x^2}+(1-a)x+a={e^x}-a(x-1)$g′(x)=ex-a.对g′(x)讨论得出结论;
(Ⅲ)设$p(x)=\frac{e}{x}-lnx,q(x)={e^{x-1}}+a-lnx$,∵$p'(x)=-\frac{e}{x^2}-\frac{1}{x}<0$,对两函数分别求导得出最值,再根据条件得出结论.
解答 解:(Ⅰ)f′(x)=f′(1)e2x-2+2x-2f(0),所以f′(1)=f′(1)+2-2f(0),即f(0)=1.
又$f(0)=\frac{f'(1)}{2}•{e^{-2}}$,所以f′(1)=2e2,所以f(x)=e2x+x2-2x.
(Ⅱ)∵f(x)=e2x-2x+x2,
∴$g(x)=f(\frac{x}{2})-\frac{1}{4}{x^2}+(1-a)x+a={e^x}+\frac{1}{4}{x^2}-x-\frac{1}{4}{x^2}+(1-a)x+a={e^x}-a(x-1)$,
∴g′(x)=ex-a.
①当a≤0时,g′(x)>0,函数g(x)在R上单调递增;
②当a>0时,由g′(x)=ex-a=0得x=lna,
∴当x∈(-∞,lna)时,g′(x)<0,g(x)单调递减;当x∈(lna,+∞)时,g′(x)>0,g(x)单调递增.
综上,当a≤0时,函数g(x)的单调递增区间为(-∞,+∞);当a>0时,函数g(x)的单调递增区间为(lna,+∞),单调递减区间为(-∞,lna).
(Ⅲ)解:设$p(x)=\frac{e}{x}-lnx,q(x)={e^{x-1}}+a-lnx$,
∵$p'(x)=-\frac{e}{x^2}-\frac{1}{x}<0$,
∴p(x)在x∈[1,+∞)上为减函数,又p(e)=0,
∴当1≤x≤e时,p(x)≥0,当x>e时,p(x)<0.
∵$q'(x)={e^{x-1}}-\frac{1}{x}$,$q''(x)={e^{x-1}}+\frac{1}{x^2}>0$,
∴q′(x)在x∈[1,+∞)上为增函数,又q′(1)=0,∴x∈[1,+∞)时,q′(x)≥0,
∴q(x)在x∈[1,+∞)上为增函数,∴q(x)≥q(1)=a+2>0.
①当1≤x≤e时,$|p(x)|-|q(x)|=p(x)-q(x)=\frac{e}{x}-{e^{x-1}}-a$,
设$m(x)=\frac{e}{x}-{e^{x-1}}-a$,则$m'(x)=-\frac{e}{x^2}-{e^{x-1}}<0$,
∴m(x)在x∈[1,+∞)上为减函数,
∴m(x)≤m(1)=e-1-a,
∵a≥2,∴m(x)<0,∴|p(x)|<|q(x)|,
∴$\frac{e}{x}$比ex-1+a更靠近lnx.
②当x>e时,$|p(x)|-|q(x)|=-p(x)-q(x)=-\frac{e}{x}+2lnx-{e^{x-1}}-a<2lnx-{e^{x-1}}-a$,
设n(x)=2lnx-ex-1-a,则$n'(x)=\frac{2}{x}-{e^{x-1}}$,$n''(x)=-\frac{2}{x^2}-{e^{x-1}}<0$,
∴n′(x)在x>e时为减函数,
∴$n'(x)<n'(e)=\frac{2}{e}-{e^{e-1}}<0$,
∴n(x)在x>e时为减函数,
∴n(x)<n(e)=2-a-ee-1<0,
∴|p(x)|<|q(x)|,
∴$\frac{e}{x}$比ex-1+a更靠近lnx.
综上:在a≥2,x≥1时,$\frac{e}{x}$比ex-1+a更靠近lnx.
点评 本题主要考查导数在函数单调性中的应用和利用导数解决不等式证明的问题,属于难度较大题型,在高考中作压轴题出现.

| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
| A. | {x|3<x≤5} | B. | {x|x≥5} | C. | {x|x<3} | D. | R |
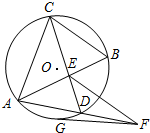 如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.
如图,已知圆O的两弦AB和CD相交于点E,FG是圆O的切线,G为切点,EF=FG.