题目内容
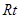 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=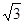 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 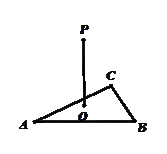
A.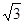 | B.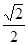 | C.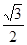 | D.2 |
D
试题分析:
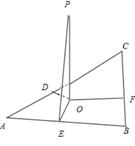
 △ABC中,∵AC=4,BC=3,
△ABC中,∵AC=4,BC=3,∴AB=5,
过O作OE⊥AB,垂足是E,作OF⊥BC,垂足是F,作OD⊥AC,交AC于D,
∵O是△ABC的内心,
∴OE=OF=OD=r,(r是△ABC内切圆半径),
∴DC=CF=r,AD=AE=4-r,BF=BE=3-r,
∴AB=3-r+4-r=5,解得r=1,
∴OE=1,
∵PO⊥面ABC,O是△ABC的内心,PO=" 3" ,OE⊥AB,
∴PE⊥AB,
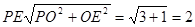 .
.∴点P到△ABC的斜边AB的距离是2.
点评:本题考查空间中点到直线的距离的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平
面问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 中,
中, 底面
底面 于
于 ,
, ,
, ,点
,点 是
是 的中点.
的中点.
 平面
平面 ;
; 与
与 所成的角为
所成的角为 ,且
,且 ,
, 的大小.
的大小.  的底面边长是
的底面边长是 ,体积是
,体积是 ,
, 分别是棱
分别是棱 、
、 的中点.
的中点.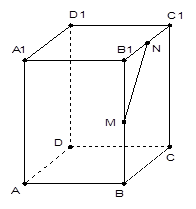
 与平面
与平面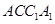 所成的角(结果用反三角函数表示);
所成的角(结果用反三角函数表示);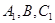 的平面与该正四棱柱所截得的多面体
的平面与该正四棱柱所截得的多面体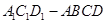 的体积.
的体积.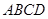 中,
中, ,
, ,点
,点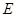 为线段
为线段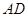 上的一点.现将
上的一点.现将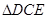 沿线段
沿线段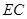 翻折到
翻折到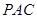 (点
(点 与点
与点 重合),使得平面
重合),使得平面 平面
平面 ,连接
,连接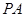 ,
, .
.
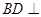 平面
平面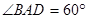 ,且点
,且点 的大小.
的大小.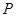 ,在直线DE上是否存在一点
,在直线DE上是否存在一点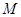 ,使得
,使得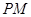 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点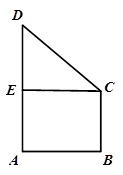
 和
和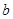 ,必定存在平面
,必定存在平面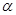 ,使得 ( )
,使得 ( )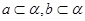
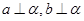
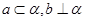
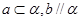
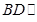 平面EFGH;
平面EFGH;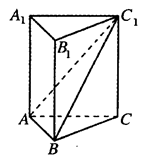
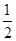
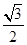
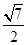
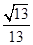
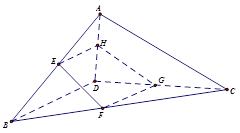
 中,D是BC的中点,
中,D是BC的中点,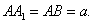
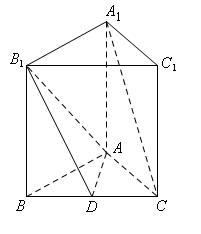
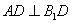 ;(Ⅱ)求证:
;(Ⅱ)求证: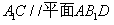 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥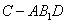 的体积.
的体积.