题目内容
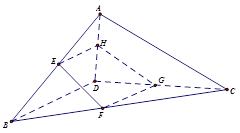
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证: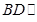 平面EFGH;
平面EFGH;
(2)求证:四边形EFGH是矩形.

(1)求证:
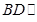 平面EFGH;
平面EFGH;(2)求证:四边形EFGH是矩形.
(1)要证明线面平行,则要根据题意,得到线线平行,即EH∥BD。
(2)证明一个四边形是矩形,首先确定是平行四边形,再证明一个角是直角来得到。
(2)证明一个四边形是矩形,首先确定是平行四边形,再证明一个角是直角来得到。
试题分析:证明:(1)∵E,H分别为AB, DA的中点.
∴EH∥BD,又
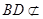 平面EFGH,
平面EFGH,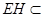 平面EFGH,
平面EFGH, 平面EFGH;……4分
平面EFGH;……4分(2)取BD中点O,连续OA,OC.
∵ AB=AD,BC=DC.∴AO⊥BD,CO⊥BD,
又AO∩CO=0.∴BD⊥平面AOC.
∴BD⊥AC. ……7分
∵E,F,G,H为AB,BC,CD,DA的中点.
∴EH∥BD,且EH=
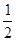 BD;FG∥BD,且FG=
BD;FG∥BD,且FG=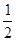 BD,EF∥AC.
BD,EF∥AC.∴EH∥FG,且EH=FG.
∴四边形EFGH是平行四边形.……10分
由(2)可知AC⊥BD,又EF∥AC,EH∥BD.
∴EF⊥EH.
∴四边形EFGH为矩形. ……12分
点评:主要是考查了空间中线面平行的证明,以及关于平面四边形的形状的确定,属于基础题。

练习册系列答案
相关题目
 中,设
中,设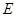 是棱
是棱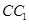 的中点.
的中点.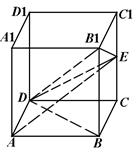
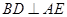 ;
;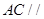 平面
平面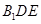 ;
;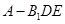 的体积.
的体积.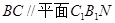 ; (2)求证:
; (2)求证: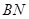
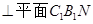 ;
; 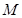 为
为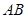 中点,在
中点,在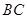 边上找一点
边上找一点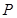 ,使
,使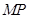
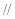 平面
平面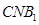 ,并求
,并求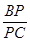 的值.
的值.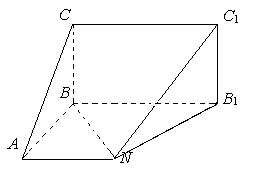
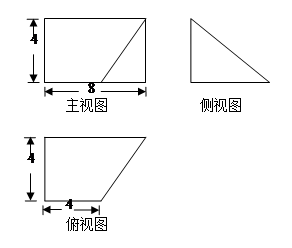
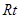 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=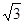 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 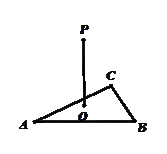
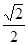
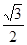
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 其中真命
其中真命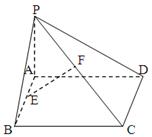
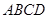 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥ ,
,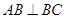 ,
, ,
, .
.
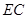 与平面
与平面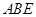 所成角的正弦值;
所成角的正弦值;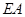 上是否存在点
上是否存在点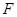 ,使
,使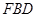 ?若存在,求出
?若存在,求出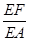 ;若不存在,说明理由.1
;若不存在,说明理由.1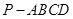 的底面为等腰梯形,
的底面为等腰梯形,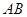 ∥
∥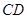 ,
,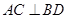 ,垂足为
,垂足为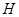 ,
,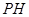 是四棱锥的高。
是四棱锥的高。
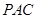
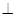 平面
平面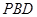 ;
;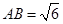 ,
,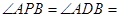 60°,求四棱锥
60°,求四棱锥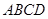 中,
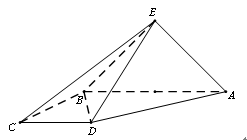
中,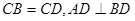 ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,