题目内容
14.在平面直角坐标系xoy中,已知经过原点O的直线l与圆C:x2+y2-4x-1=0交于A,B两点.(1)若直线m:ax-2y+a+2=0(a>0)与圆C相切,切点为B,求直线l的方程;
(2)若OB=2OA,求直线l的方程;
(3)若圆C与x轴的正半轴的交点为D,求△ABD面积的最大值.
分析 (1)由直线与圆C相切d=r,求出直线m的方程,得切点B的坐标,从而求出直线l的方程;
(2)设出直线AB的方程,利用圆心到直线AB的距离与半径、弦长的关系,求出直线方程即可;
(3)求出点D的坐标,写出△ABD的面积表达式,利用直线AB的方程与圆C的方程联立,求出面积的最大值.
解答 解:(1)由直线m:ax-2y+a+2=0(a>0)与圆C相切,
圆心为(2,0),半径为$\sqrt{5}$;
∴$\frac{{|{3a+2}|}}{{\sqrt{{a^2}+4}}}=\sqrt{5}$;
化简得:a2+3a-4=0,
解得a=1或a=-4,
又a>0,故a=1;
∴直线m:x-2y+3=0
与圆C联立,得$\left\{\begin{array}{l}{x-2y+3=0}\\{{x}^{2}{+y}^{2}-4x-1=0}\end{array}\right.$;
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即切点B(1,2);
∴直线l的方程为:y=2x;
(2)取AB中点M,则$AM=\frac{1}{2}AB$,
又$OA=\frac{1}{3}AB$,所以$OM=\frac{1}{3}AM$;
设:OM=x,圆心C(2,0)到直线l的距离为d,
由勾股定理得:x2+d2=4,9x2+d2=5,
解得${d^2}=\frac{31}{8}$;
设所求直线l的方程为y=kx,
∴$d=\frac{{|{2k}|}}{{\sqrt{1+{k^2}}}}$,
解得$k=±\sqrt{31}$,
∴直线l的方程为:y=±$\sqrt{31}$x;
(3)如图所示: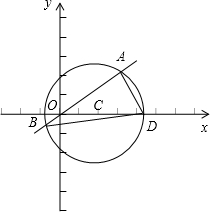
设A,B两点的纵坐标分别为y1,y2,
易知$D(2+\sqrt{5},0)$,
${S_{△ABD}}=\frac{1}{2}(2+\sqrt{5})(|{y_1}|+|{y_2}|)$,
易知|y1|+|y2|=|y1-y2|;
设AB的方程为x=ty,
由$\left\{\begin{array}{l}x=ty\\{x^2}+{y^2}-4x-1=0\end{array}\right.$,
消去x得(t2+1)y2-4ty-1=0,
$|{{y_1}-{y_2}}|=\frac{{\sqrt{△}}}{{1+{t^2}}}=\frac{{\sqrt{20{t^2}+4}}}{{1+{t^2}}}$=$2\sqrt{\frac{{5{t^2}+1}}{{{{({t^2}+1)}^2}}}}$,
设x=5t2+1,则|y1-y2|=2$\sqrt{\frac{25x}{{x}^{2}+8x+16}}$=2$\sqrt{\frac{25}{x+\frac{16}{x}+8}}$≤$\frac{5}{2}$,(当且仅当x=4时取等号),
∴△ABD面积最大值为$\frac{1}{2}$(2+$\sqrt{5}$)•$\frac{5}{2}$=$\frac{5}{4}$(2+$\sqrt{5}$).
点评 本题考查了直线与圆的综合应用问题,也考查了勾股定理的应用问题,考查了根与系数的应用问题,考查了分析问题与解决问题的能力,是综合性题目.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | $(x-1+\sqrt{3}i)(x-1-\sqrt{3}i)$ | B. | $(\sqrt{2}x-\sqrt{2}+\sqrt{3}i)(\sqrt{2}x-\sqrt{2}-\sqrt{3}i)$ | C. | 2(x-1+i)(x-1-i) | D. | 2(x+1+i)(x+1-i) |
| A. | $\sqrt{74}$ | B. | 3$\sqrt{10}$ | C. | $\sqrt{14}$ | D. | $\sqrt{53}$ |
| A. | x1x2>1 | B. | x1x2=1 | C. | 0<x1x2<1 | D. | x1x2<0 |
| A. | 不存在 | B. | 与x轴平行或重合 | C. | 与x轴垂直 | D. | 与x轴相交不垂直 |
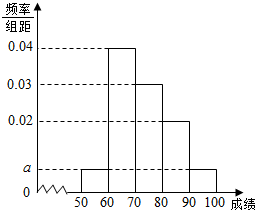 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].