题目内容
【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且（a+b+c）（a+b﹣c）=3ab．
（Ⅰ）求角C的值；
（Ⅱ）若c=2，且△ABC为锐角三角形，求a+b的取值范围．
【答案】解：（Ⅰ）△ABC中，（a+b+c）（a+b﹣c）=3ab，
∴a2+b2﹣c2=ab，
由余弦定理得，cosC= 
= 
；
又∵C∈（0，π），
∴C= 
；
（Ⅱ）由c=2，C= ，根据正弦定理得，
= 
= 
= 
= 
，
∴a+b= （sinA+sinB）
= [sinA+sin（ 
﹣A）]
=2 
sinA+2cosA
=4sin（A+ 
）；
又∵△ABC为锐角三角形，
∴ 
，
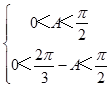解得 ＜A＜ 
；
∴ ＜A+ ＜ ，
∴2 ＜4sin（A+ ）≤4，
综上，a+b的取值范围是（2 ，4]
【解析】（Ⅰ）化简（a+b+c）（a+b﹣c）=3ab，利用余弦定理求得C的值；（Ⅱ）由正弦定理求出a+b的解析式，利用三角恒等变换化简，根据题意求出A的取值范围，从而求出a+b的取值范围．
【考点精析】根据题目的已知条件，利用余弦定理的定义的相关知识可以得到问题的答案，需要掌握余弦定理:
;
;
．
练习册系列答案
相关题目
【题目】已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 
= 
x+ 
，据此模型预报广告费用为8万元时的销售额是（ ）
附： = 
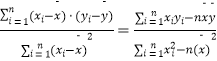； = ﹣ x．
A.59.5
B.52.5
C.56
D.63.5
