题目内容
12.函数y=f(x)为偶函数,满足f(x))=f(x-2),且当x∈[0,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=log4|x|的图象的交点共有( )| A. | 6个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据条件求出函数是周期为2的函数,求出一个周期内的图象,作出两个函数的图象,利用数形结合即可得到结论.
解答 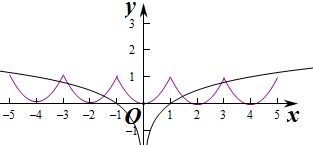 解:由f(x)=f(x-2),得函数f(x)是周期为2的函数,
解:由f(x)=f(x-2),得函数f(x)是周期为2的函数,
设x∈[-1,0],则-x∈[0,1],
∵当x∈[0,1]时,f(x)=x2,
∴当-x∈[0,1]时,f(-x)=(-x)2=x2,
∵y=f(x)为偶函数,∴f(-x)=f(x)=x2,
即当x∈[-1,1]时,f(x)=x2,
作出函数f(x)=x2,与y=log4|x|的图象,
当x>0时,设y=g(x)=log4|x|=log4x,
则g(3)=log43<1,f(3)=f(1)=1,
g(5)=log45>1,故当x>0,两个函数有3个交点,
根据偶函数的对称性知两个图象的交点个数为6个,
故选:A.
点评 本题主要考查函数交点个数的判断,利用条件判断函数的周期性,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
3.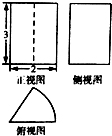 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )| A. | 2π | B. | π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
20.七位裁判各自对一名跳水运动员打分后,去掉一个最高分,再去掉一个最低分,关于剩余分数的说法一定正确的是( )
| A. | 众数不变 | B. | 方差不变 | C. | 平均值不变 | D. | 中位数不变 |
1.“x>1”是“︳x|>1”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
2.在如图所示的四个图示中,是结构图的是( )
| A. | 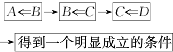 | B. | 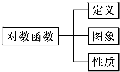 | ||
| C. |  | D. |  |