题目内容
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)判断曲线![]() 是否位于
是否位于![]() 轴下方,并说明理由.
轴下方,并说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)见解析.
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(1)求导![]() ,得到切线斜率
,得到切线斜率![]() ,利用点斜式得到直线的方程;(2)“要证明
,利用点斜式得到直线的方程;(2)“要证明![]() ”等价于“
”等价于“![]() ”,构造新函数确定函数的最小值大于等于
”,构造新函数确定函数的最小值大于等于![]() ;(3)曲线
;(3)曲线![]() 是位于
是位于![]() 轴下方即证明
轴下方即证明![]() )
)![]() ,利用(Ⅱ)可知
,利用(Ⅱ)可知![]() ,转证
,转证![]() 即可.
即可.
试题解析:
函数的定义域为![]() ,
,
![]() .
.
(Ⅰ)![]() ,又
,又![]() ,
,
曲线![]() 在
在![]() 处的切线方程为
处的切线方程为
![]() ,
,
即![]() .
.
(Ⅱ)“要证明![]() ”等价于“
”等价于“![]() ”
”
设函数![]() .
.
令![]() ,解得
,解得![]() .
.
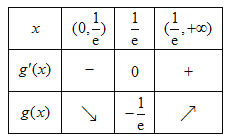
因此,函数![]() 的最小值为
的最小值为![]() .故
.故![]() .
.
即![]() .
.
(Ⅲ)曲线![]() 位于
位于![]() 轴下方. 理由如下:
轴下方. 理由如下:
由(Ⅱ)可知![]() ,所以
,所以![]() .
.
设![]() ,则
,则![]() .
.
令![]() 得
得![]() ;令
;令![]() 得
得![]() .
.
所以![]() 在
在![]() 上为增函数,
上为增函数, ![]() 上为减函数.
上为减函数.
所以当![]() 时,
时, ![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时,
时, ![]() .
.
又因为![]() , 所以
, 所以![]() 恒成立.
恒成立.
故曲线![]() 位于
位于![]() 轴下方.
轴下方.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表数据:
单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为 ![]() =﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
=﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
【题目】某品牌连锁便利店有![]() 个分店,A,B,C三种商品在各分店均有销售,这三种商品的单价和重量如表1所示:
个分店,A,B,C三种商品在各分店均有销售,这三种商品的单价和重量如表1所示:
商品A | 商品B | 商品C | |
单价(元) | 15 | 20 | 30 |
每件重量(千克) | 0.2 | 0.3 | 0.4 |
表1
某日总店向各分店分配的商品A,B,C的数量如表2所示:
商品 分店 | 分店1 | 分店2 | …… | 分店 |
A | 12 | 20 | m1 | |
B | 15 | 20 | m2 | |
C | 20 | 15 | m3 |
表2
表3表示该日分配到各分店去的商品A,B,C的总价和总重量:
分店1 | 分店2 | …… | 分店 | |
总价(元) |
| |||
总重量(千克) |
|
表3
则![]() __________ ;
__________ ; ![]() __________ .
__________ .