题目内容
【题目】下列四组函数中，表示同一函数的是（ ）
A.f（x）=x0与g（x）=1
B.f（x）=x与g（x）= 
C.f（x）=x2﹣1与g（x）=x2+1
D.f（x）=|x|与g（x）= 
【答案】D
【解析】解：对于A：f（x）=x0的定义域为{x|x≠0}，而g（x）=1定义域为R，它们的定义域不同，∴不是同一函数； 对于B：f（x）=x的定义域为R，而g（x）= 
定义域为{x|x≠0}，它们的定义域不同，∴不是同一函数；
对于C：f（x）=x2﹣1和g（x）=x2+1的定义域都是R，它们的定义域相同，但对应关系不同，∴不是同一函数；
对于D：f（x）=|x|和g（x）= 
的定义域都是R，它们的定义域相同，对应关系也相同，∴是同一函数；
故选D．
【考点精析】利用判断两个函数是否为同一函数对题目进行判断即可得到答案，需要熟知只有定义域和对应法则二者完全相同的函数才是同一函数．
练习册系列答案
相关题目
【题目】已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，
x | ﹣1 | 0 | 4 |
f（x） | 1 | 2 | 2 |
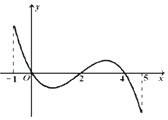
f（x）的导函数y=f′（x）的图象（该图象关于（2，0）中心对称） 如图所示．
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）﹣a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[﹣1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在a=1是上凸的
其中一定正确命题的序号是 ． 