题目内容
【题目】已知函数f（x）=x2﹣x+c（c∈R）的一个零点为1． （Ⅰ）求函数f（x）的最小值；
（Ⅱ）设 
，若g（t）=2，求实数t的值．
【答案】解：（Ⅰ）∵函数f（x）=x2﹣x+c的一个零点为1， ∴f（1）=0，即12﹣1+c=0，解得c=0，
∴ 
，
∴当 
时，函数f（x）的最小值为- 
．
（Ⅱ）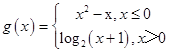 
，
∵g（t）=2，
∴当t≤0时，g（t）=t2﹣t=2，解得t=﹣1，或t=2（舍去）；
当t＞0时，g（t）=log2（t+1）=2，解得t=3．
综上所述，实数t的值为﹣1或3．
【解析】（Ⅰ）由已知可得f（1）=0，易求c，配方后利用二次函数的性质可求最小值；（Ⅱ）分t≤0，t＞0两种情况讨论，表示出方程g（t）=2可解t值；
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
练习册系列答案
相关题目
