Question

【题目】设函数，（其中，，），在上既无最大值，也无最小值，且，则下列结论成立的是（ ）

A.若对任意，则

B.的图象关于点中心对称

C.函数的单调减区间为

D.函数的图象相邻两条对称轴之间的距离是

Answer 1

【答案】C

【解析】

由函数满足的条件先求出函数解析式，根据解析式及三角函数的图象与性质可分析各选项的正误,即可求解.

∵在上既无最大值，也无最小值，

∴是函数的一个单调区间，区间长度为，

即函数的周期，

即，则.

∵，

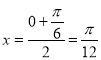∴是函数的一条对称轴，

∵，

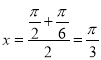∴，即是函数的一个对称中心，

则①，

②，

由①②得，

又，

∴，

又，则有时，，

即，函数的周期.

对于A：若对任意实数恒成立，

则为函数的最小值，为函数的最大值，

则，故A错误；

对于B：时，，不对称，故B错误；

对于C：当，则，则此时函数单调递减，即函数在每一个上单调递减，故C正确.

对于D：对于函数的图象，相邻两条对称轴之间的距离是,故D错误，

故选:C.