题目内容
【题目】在直角坐标系中，圆
：
经过伸缩变换
，后得到曲线
以坐标原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线l的极坐标方程为
求曲线的直角坐标方程及直线l的直角坐标方程；
在上求一点M，使点M到直线l的距离最小，并求出最小距离．
【答案】（1）
； （2）
.
【解析】
（1）由
后得到曲线C2，可得：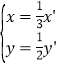
，代入圆C1：x2+y2=1，化简可得曲线C2的直角坐标方程，将直线l的极坐标方程为cosθ+2sinθ=
化为：ρcosθ+2ρsinθ=10，进而可得直线l的直角坐标方程.
（2）将直线x+2y﹣10=0平移与C2相切时，则第一象限内的切点M满足条件，联立方程求出M点的坐标，进而可得答案.
（1）因为
后得到曲线
，
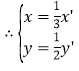，代入圆
：
得：
，
故曲线的直角坐标方程为；
直线l的极坐标方程为
．
即
，即.
将直线平移与相切时，则第一象限内的切点M满足条件，
设过M的直线为
，
则由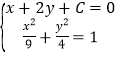
得：
，
由
得：
故
，或
，
舍去
，
则
，即M点的坐标为
，
则点M到直线l的距离
练习册系列答案
三点一测快乐周计划系列答案
相关题目
