题目内容
【题目】如图，AOB是一块半径为r的扇形空地，
．某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH，剩余的地方进行绿化．若
，设
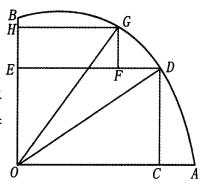
(Ⅰ)记活动场地与停车场占地总面积为
，求的表达式；
(Ⅱ)当
为何值时，可使活动场地与停车场占地总面积最大．
【答案】（Ⅰ）
其中
；
（Ⅱ）
时，可使活动场地与停车场占地总面积最大．
【解析】
（Ⅰ）由题意求得矩形
和矩形
的面积（Ⅱ）求
的导数
，利用
,
判断的单调性，求最大值即可.
Ⅰ
由题意得，在矩形OCDE中，
，
，
，
矩形OCDE的面积为
；
又
，四边形EFGH是矩形，
，
，
；
矩形EFGH的面积为
，
，其中；
Ⅱ由题意知，
，
令，得
，
解得，或
不合题意，舍去；
令
，则
；
当
时，
，单调递增；
当
时，
，单调递减；
当
时，取得最大值；
即时，可使活动场地与停车场占地总面积最大．
练习册系列答案
发散思维新课堂系列答案
相关题目
