题目内容
已知等比数列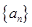 前
前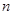 项和为
项和为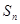 ,且满足
,且满足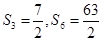 ,
,
(Ⅰ)求数列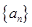 的通项公式;
的通项公式;
(Ⅱ)求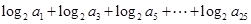 的值.
的值.
(1)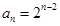 ;(2)143.
;(2)143.
解析试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和及对数式的运算等数学知识,考查思维能力、分析问题解决问题的能力以及计算能力.第一问,法一:利用等比数列的前n项和公式,将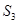 和
和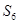 展开,组成方程组,两式相除,解出
展开,组成方程组,两式相除,解出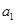 和
和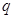 ,写出通项公式;法二:利用等比数列的通项公式,又因为
,写出通项公式;法二:利用等比数列的通项公式,又因为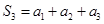 ,
,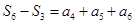 ,展开,相除,解出
,展开,相除,解出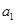 和
和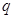 ,写出通项公式;第二问,先将第一问的结论代入,化简
,写出通项公式;第二问,先将第一问的结论代入,化简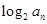 ,得到
,得到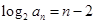 ,所以可以证出数列
,所以可以证出数列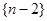 为等差数列,所以利用等差数列的前n项和公式进行求和化简.
为等差数列,所以利用等差数列的前n项和公式进行求和化简.
试题解析:(1)法一: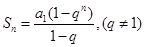
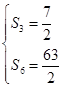 ,整理得
,整理得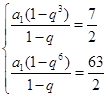 ,解得
,解得 ,
,
得 ,
,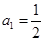 ,所以,通项公式为
,所以,通项公式为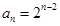 5分
5分
法二: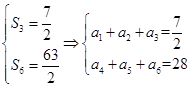 ,得
,得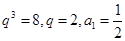 ,所以,通项公式为
,所以,通项公式为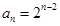 . 5分
. 5分
(2)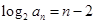 6分
6分
则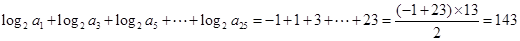 12分
12分
考点:1.等比数列的通项公式;2.等比数列的前n项和公式;3.对数式的运算;4.等差数列的前n项和公式.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, .
. log2an+1 ,求数列
log2an+1 ,求数列 的前
的前 。
。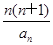 ,求实数λ的最大值.
,求实数λ的最大值. ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.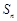 是等比数列
是等比数列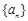 的前
的前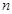 项和,
项和,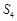 、
、 、
、 成等差数列,且
成等差数列,且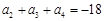 .
.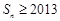 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有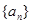 的前
的前 项和
项和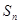 ,已知
,已知 ,
,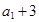 ,
,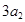 ,
,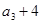 成等差数列.
成等差数列.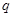 和通项
和通项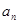 ;
;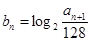 ,求
,求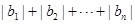 .
.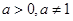 ,数列
,数列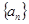 是首项为
是首项为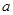 ,公比也为
,公比也为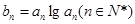
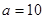 ,求数列
,求数列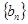 的前
的前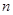 项和
项和 ;
; 单调递增,
单调递增,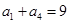 ,
,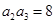 ,
, .
.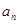 ;
; ,求
,求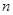 的最小值.
的最小值.