题目内容
已知等比数列 单调递增,
单调递增,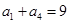 ,
,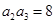 ,
, .
.
(Ⅰ)求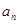 ;
;
(Ⅱ)若 ,求
,求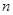 的最小值.
的最小值.
(Ⅰ) 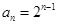 ;(Ⅱ)
;(Ⅱ) 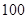 .
.
解析试题分析:(Ⅰ)先由已知条件根据函数根的性质构造函数求出函数的根,那么就得到等比数列的第一项和第四项,由等比数列的形式即得数列的通项;(Ⅱ)首先求出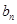 的通项公式,然后代入
的通项公式,然后代入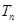 得不等式,解不等式即可,注意
得不等式,解不等式即可,注意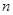 的取值集合.
的取值集合.
试题解析:解:(Ⅰ)因为 是等比数列,所以
是等比数列,所以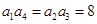 , 2分
, 2分
又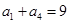 ,所以
,所以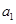 ,
,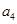 是方程
是方程 ,
,
又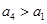 ,所以
,所以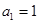 ,
,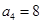 4分
4分
所以公比 ,从而
,从而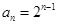 6分
6分
(Ⅱ)由上知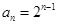 ,所以
,所以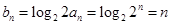 8分
8分
所以有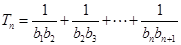
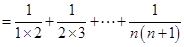
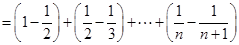
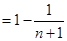 12分
12分
由 ,得
,得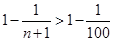 ,
,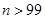
所以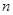 的最小值是
的最小值是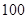 14分
14分
考点:1、等比数列的通项公式;2、数列与函数的综合应用;3、数列与不等式的综合应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 前
前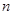 项和为
项和为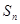 ,且满足
,且满足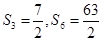 ,
,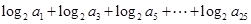 的值.
的值. 元,第n+l个月月底余
元,第n+l个月月底余 元,写出a1的值并建立
元,写出a1的值并建立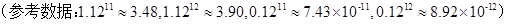
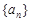 满足
满足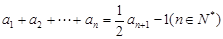 .
. 与
与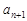 之间插入
之间插入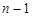 个数连同
个数连同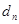 (
(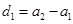 )的等差数列.
)的等差数列.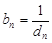 ,求数列
,求数列 的前
的前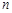 和
和 ;
;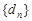 中是否存在三项
中是否存在三项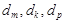 (其中
(其中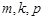 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.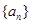 满足
满足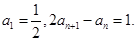
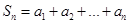
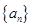 中,
中,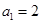 ,
,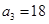 ,等差数列
,等差数列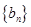 中,
中,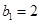 ,且
,且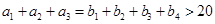 .
.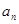 ;
;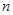 项和
项和 .
.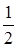 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n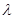 ·bn+1(
·bn+1(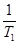 +
+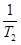 +
+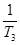 + +
+ +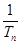 与
与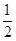 Sn的大小.
Sn的大小.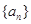 的所有项均为正数,首项
的所有项均为正数,首项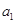 =1,且
=1,且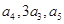 成等差数列.
成等差数列.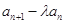 }的前
}的前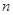 项和为
项和为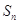 ,若
,若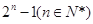 ,求实数
,求实数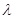 的值.
的值.