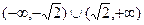题目内容
已知函数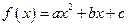
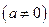 满足
满足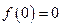 ,对于任意
,对于任意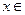 R都有
R都有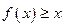 ,且
,且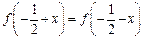 ,令
,令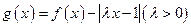 .
.
(1)求函数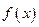 的表达式;
的表达式;
(2)求函数 的单调区间;
的单调区间;
(3)研究函数 在区间
在区间 上的零点个数.
上的零点个数.
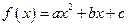
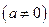 满足
满足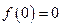 ,对于任意
,对于任意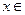 R都有
R都有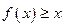 ,且
,且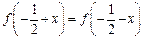 ,令
,令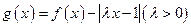 .
.(1)求函数
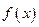 的表达式;
的表达式;(2)求函数
 的单调区间;
的单调区间;(3)研究函数
 在区间
在区间 上的零点个数.
上的零点个数.(1) 解:∵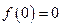 ,∴
,∴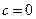 . … 1分
. … 1分
∵对于任意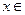 R都有
R都有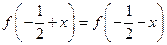 ,
,
∴函数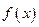 的对称轴为
的对称轴为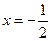 ,即
,即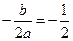 ,得
,得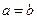 . …… 2分
. …… 2分
又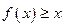 ,即
,即 对于任意
对于任意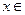 R都成立,∴
R都成立,∴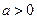 ,且
,且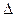
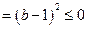 .
.
∵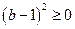 , ∴
, ∴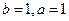 . ∴
. ∴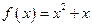 . …… 4分
. …… 4分
(2) 解: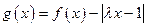
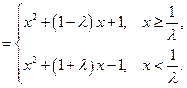 …… 5分
…… 5分
① 当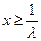 时,函数
时,函数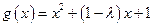 的对称轴为
的对称轴为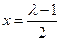 ,
,
若 ,即
,即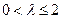 ,函数
,函数 在
在 上单调递增;…… 6分
上单调递增;…… 6分
若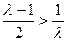 ,即
,即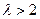 ,函数
,函数 在
在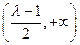 上单调递增,在
上单调递增,在 上单调递减.…… 7分
上单调递减.…… 7分
② 当 时,函数
时,函数 的对称轴为
的对称轴为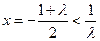 ,
,
则函数 在
在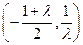 上单调递增,在
上单调递增,在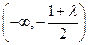 上单调递减.… 8分
上单调递减.… 8分
综上所述,当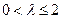 时,函数
时,函数 单调递增区间为
单调递增区间为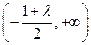 ,
,
单调递减区间为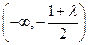 ; …… 9分
; …… 9分
当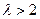 时,函数
时,函数 单调递增区间为
单调递增区间为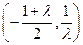 和
和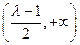 ,
,
单调递减区间为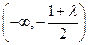 和
和 .… 10分
.… 10分
(3)解:① 当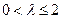 时,由(2)知函数
时,由(2)知函数 在区间
在区间 上单调递增,
上单调递增,
又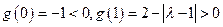 ,
,
故函数 在区间
在区间 上只有一个零点. …… 11分
上只有一个零点. …… 11分
② 当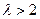 时,则
时,则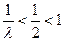 ,而
,而
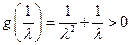 ,
,
 ,
,
(ⅰ)若 ,由于
,由于 ,
,
且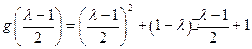
 ,
,
此时,函数 在区间
在区间 上只有一个零点; 12分
上只有一个零点; 12分
(ⅱ)若 ,由于
,由于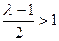 且
且
 ,此时,函数
,此时,函数 在区间
在区间
上有两个不同的零点. …… 13分
综上所述,当 时,函数
时,函数 在区间
在区间 上只有一个零点;
上只有一个零点;
当 时,函数
时,函数 在区间
在区间 上有两个不同的零点. …… 14分
上有两个不同的零点. …… 14分
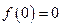 ,∴
,∴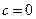 . … 1分
. … 1分 ∵对于任意
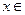 R都有
R都有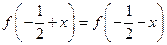 ,
,∴函数
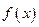 的对称轴为
的对称轴为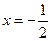 ,即
,即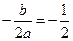 ,得
,得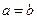 . …… 2分
. …… 2分又
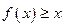 ,即
,即 对于任意
对于任意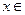 R都成立,∴
R都成立,∴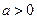 ,且
,且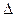
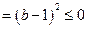 .
.∵
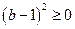 , ∴
, ∴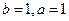 . ∴
. ∴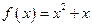 . …… 4分
. …… 4分(2) 解:
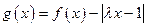
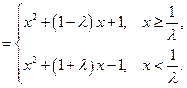 …… 5分
…… 5分① 当
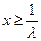 时,函数
时,函数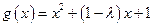 的对称轴为
的对称轴为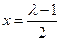 ,
,若
 ,即
,即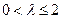 ,函数
,函数 在
在 上单调递增;…… 6分
上单调递增;…… 6分若
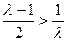 ,即
,即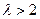 ,函数
,函数 在
在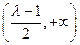 上单调递增,在
上单调递增,在 上单调递减.…… 7分
上单调递减.…… 7分② 当
 时,函数
时,函数 的对称轴为
的对称轴为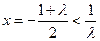 ,
,则函数
 在
在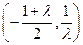 上单调递增,在
上单调递增,在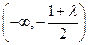 上单调递减.… 8分
上单调递减.… 8分综上所述,当
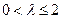 时,函数
时,函数 单调递增区间为
单调递增区间为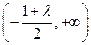 ,
,单调递减区间为
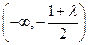 ; …… 9分
; …… 9分当
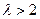 时,函数
时,函数 单调递增区间为
单调递增区间为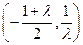 和
和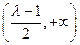 ,
,单调递减区间为
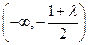 和
和 .… 10分
.… 10分(3)解:① 当
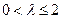 时,由(2)知函数
时,由(2)知函数 在区间
在区间 上单调递增,
上单调递增,又
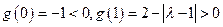 ,
,故函数
 在区间
在区间 上只有一个零点. …… 11分
上只有一个零点. …… 11分② 当
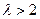 时,则
时,则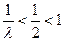 ,而
,而
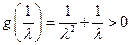 ,
, ,
,(ⅰ)若
 ,由于
,由于 ,
,且
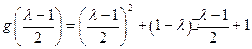
 ,
,此时,函数
 在区间
在区间 上只有一个零点; 12分
上只有一个零点; 12分(ⅱ)若
 ,由于
,由于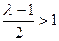 且
且
 ,此时,函数
,此时,函数 在区间
在区间
上有两个不同的零点. …… 13分
综上所述,当
 时,函数
时,函数 在区间
在区间 上只有一个零点;
上只有一个零点;当
 时,函数
时,函数 在区间
在区间 上有两个不同的零点. …… 14分
上有两个不同的零点. …… 14分略

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
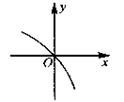
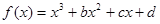 图象如图,则函数
图象如图,则函数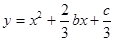 的单调递增区间为( )
的单调递增区间为( )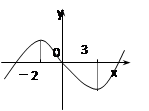

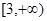

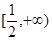
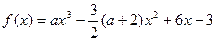 .
.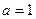 时,求函数
时,求函数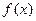 的极小值;
的极小值; )试讨论曲线
)试讨论曲线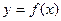 与
与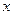 轴的公共点的个数。
轴的公共点的个数。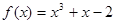 在
在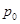 处的切线平行于直线
处的切线平行于直线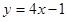 ,则
,则
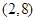

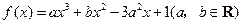 在
在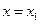 ,
,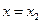 处取得极值,且
处取得极值,且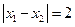 .
.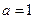 ,求
,求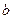 的值,并求
的值,并求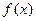 的单调区间;
的单调区间;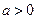 ,求
,求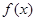 ,若满足
,若满足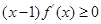 ,则必有( )
,则必有( )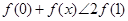


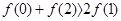
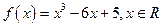
 的方程
的方程 有三个不同的实根,求实数
有三个不同的实根,求实数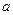 的取值范围。
的取值范围。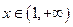 时,
时,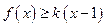 恒成立。求实数
恒成立。求实数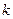 的取值范围。
的取值范围。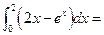
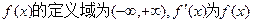 的导函数,函数
的导函数,函数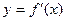 的图象如图所示,且
的图象如图所示,且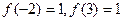 ,则不等式
,则不等式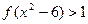 的
的 解集为( **
解集为( ** *)
*)