题目内容
((本小题12分)
设函数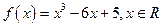
(1)若关于 的方程
的方程 有三个不同的实根,求实数
有三个不同的实根,求实数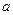 的取值范围。
的取值范围。
(2)当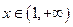 时,
时,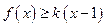 恒成立。求实数
恒成立。求实数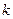 的取值范围。
的取值范围。
设函数
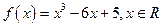
(1)若关于
 的方程
的方程 有三个不同的实根,求实数
有三个不同的实根,求实数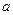 的取值范围。
的取值范围。(2)当
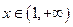 时,
时,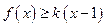 恒成立。求实数
恒成立。求实数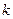 的取值范围。
的取值范围。解:① 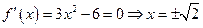
所以函数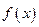 的极大值为
的极大值为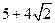 ,极小值为
,极小值为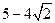
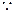 关于
关于 的方程
的方程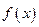 =
=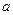 有三个不同的实根
有三个不同的实根
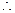
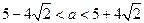
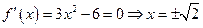
 | 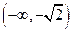 | 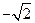 | 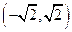 | 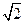 | 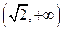 |
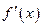 | 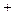 | | 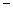 | | 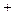 |
| | 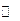 | 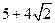 |  | 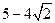 |  |
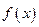 的极大值为
的极大值为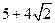 ,极小值为
,极小值为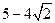
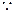 关于
关于 的方程
的方程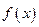 =
=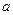 有三个不同的实根
有三个不同的实根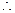
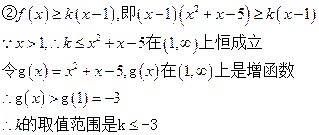
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
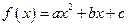
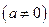 满足
满足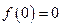 ,对于任意
,对于任意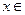 R都有
R都有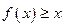 ,且
,且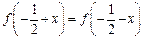 ,令
,令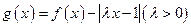 .
.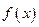 的表达式;
的表达式; 的单调区间;
的单调区间; 上的零点个数.
上的零点个数.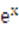 -kx,.
-kx,. (2)若k>0,且对于任意
(2)若k>0,且对于任意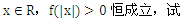 确定实数k的取值范围;
确定实数k的取值范围;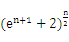 (
(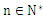 )。
)。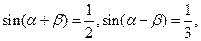 则
则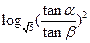 等于 ( )
等于 ( )  在点
在点 处的切线方程是
处的切线方程是 ,则----------------( )
,则----------------( ) ,则函数
,则函数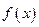 在
在 处的导数
处的导数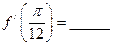
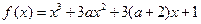 有极大值和极小值,则
有极大值和极小值,则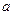 的取值范围是 ( )
的取值范围是 ( )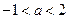
 或
或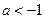
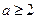 或
或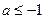
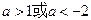
 .
. 时,恒有
时,恒有 ,试求实数a的取值范围;
,试求实数a的取值范围; ,试证明:
,试证明: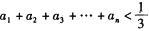
 在
在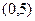 上是
上是
 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;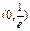 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.