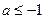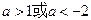题目内容
(14分)
设函数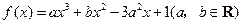 在
在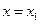 ,
,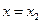 处取得极值,且
处取得极值,且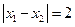 .
.
(Ⅰ)若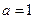 ,求
,求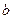 的值,并求
的值,并求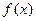 的单调区间;
的单调区间;
(Ⅱ)若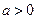 ,求
,求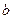 的取值范围.
的取值范围.
设函数
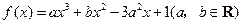 在
在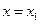 ,
,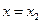 处取得极值,且
处取得极值,且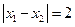 .
.(Ⅰ)若
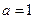 ,求
,求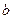 的值,并求
的值,并求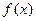 的单调区间;
的单调区间;(Ⅱ)若
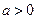 ,求
,求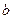 的取值范围.
的取值范围.
(Ⅱ)由①式及题意知
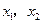 为方程
为方程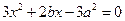 的两根,
的两根,所以
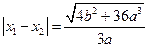 .从而
.从而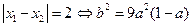 ,
,由上式及题设知
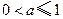 .························· 8分
.························· 8分考虑
 ,
,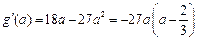 . ………………………10分
. ………………………10分故
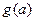 在
在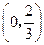 单调递增,在
单调递增,在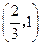 单调递减,从而
单调递减,从而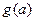 在
在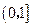 的极大值为
的极大值为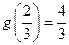
 .
.又
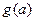 在
在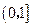 上只有一个极值,所以
上只有一个极值,所以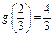 为
为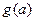 在
在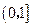 上的最大值,且最小值为
上的最大值,且最小值为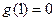 ………………………………12分
………………………………12分所以
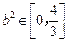 ,即
,即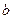 的取值范围为
的取值范围为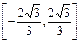 ………………14分
………………14分法二:
由①式及题意知
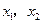 为方程
为方程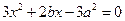 的两根,
的两根,所以
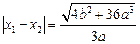 .从而
.从而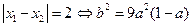 ,
,由上式及题设知
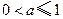 . ……………………………8分
. ……………………………8分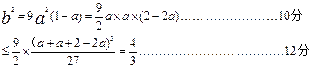
所以
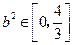 ,即
,即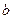 的取值范围为
的取值范围为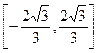 ………………14分
………………14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
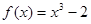 在P0点处的切线平行于直线
在P0点处的切线平行于直线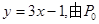 点的坐标为( )
点的坐标为( )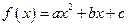
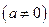 满足
满足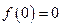 ,对于任意
,对于任意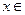 R都有
R都有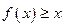 ,且
,且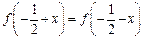 ,令
,令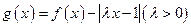 .
.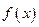 的表达式;
的表达式; 的单调区间;
的单调区间; 上的零点个数.
上的零点个数.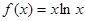 的单调增区间为
的单调增区间为 
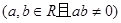 的图象如图所示,且
的图象如图所示,且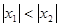 ,则有
,则有
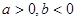
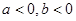
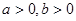
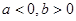
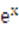 -kx,.
-kx,. (2)若k>0,且对于任意
(2)若k>0,且对于任意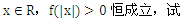 确定实数k的取值范围;
确定实数k的取值范围;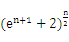 (
(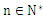 )。
)。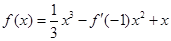 ,则(
,则(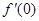 +
+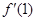 )
) =
=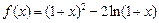 .
.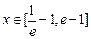 时,不等式
时,不等式
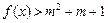 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;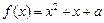 在区间[0,2]上恰好有两个相异的实根,求实数
在区间[0,2]上恰好有两个相异的实根,求实数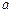 的取值范围.
的取值范围.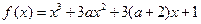 有极大值和极小值,则
有极大值和极小值,则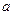 的取值范围是 ( )
的取值范围是 ( )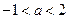
 或
或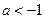
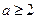 或
或