题目内容
【题目】
在平面直角坐标系
中，椭圆
：
的右焦点为
（
，
为常数），离心率等于0.8，过焦点
、倾斜角为
的直线
交椭圆于
、
两点．
⑴求椭圆的标准方程；
⑵若
时，
，求实数；
⑶试问
的值是否与的大小无关，并证明你的结论．
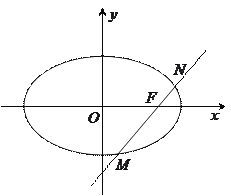
【答案】（1）
（2）
（3）
为定值
【解析】
试题（1）利用待定系数法可得，椭圆方程为；
（2）我们要知道
=
的条件应用，在于直线
交椭圆两交点M，N的横坐标为
，这样代入椭圆方程，容易得到
，从而解得；
（3） 需讨论斜率是否存在．一方面斜率不存在即=时，由（2）得；另一方面，当斜率存在即
时，可设直线的斜率为
，得直线MN：
，联立直线与椭圆方程，利用韦达定理和焦半径公式，就能得到，所以为定值，与直线的倾斜角的大小无关
试题解析：（1）
，
得：
，椭圆方程为
（2）当时，
，得：
，
于是当=时，
，于是
，
得到
（3）①当=时，由（2）知
②当时，设直线的斜率为，
，
则直线MN：
联立椭圆方程有
，
，
，
=
+
=
=
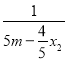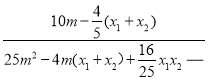得
综上，为定值，与直线的倾斜角的大小无关
练习册系列答案
相关题目
