题目内容
【题目】已知双曲线E：
－
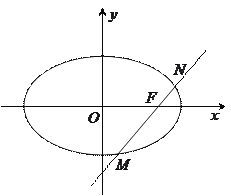
＝1(a>0，b>0)的右顶点为A，O为坐标原点，M为OA的中点，若以AM为直径的圆与E的渐近线相切，则双曲线E的离心率等于（ ）
A.
B.
C.
D.
【答案】A
【解析】
根据双曲线的方程和其几何性质得出以AM为直径的圆的圆心的坐标为
，半径r＝
，再由圆心到双曲线的渐近线的距离建立关于
的方程，再根据双曲线的离心率公式可得选项.
由题意知，双曲线E的右顶点为A(a，0)，渐近线方程为y＝±
x，即bx±ay＝0.
由M为OA的中点，可知
．
故以AM为直径的圆的圆心的坐标为，半径r＝，|AM|＝
，
又双曲线的渐近线与圆相切，所以圆心到渐近线的距离等于圆的半径，即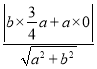
＝，
整理得
＝3b，即c＝3
，即
，
从而得e2＝
，所以e＝
，
故选：A.
练习册系列答案
相关题目
【题目】杨辉三角，是二项式系数在三角形中的一种几何排列.中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现了杨辉三角.在欧洲，帕斯卡在1654年也发现了这一规律，所以这个表又叫做帕斯卡三角形.杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合.
第0行 | 1 |
第1行 | 1 1 |
第2行 | 1 2 1 |
第3行 | 1 3 3 1 |
第4行 | 1 4 6 4 1 |
第5行 | 1 5 10 10 5 1 |
第6行 | 1 6 15 20 15 6 1 |
（1）记杨辉三角的前n行所有数之和为
，求的通项公式；
（2）在杨辉三角中是否存在某一行，且该行中三个相邻的数之比为
？若存在，试求出是第几行；若不存在，请说明理由；
（3）已知n，r为正整数，且
.求证：任何四个相邻的组合数
，
，
，
不能构成等差数列.
