题目内容
【题目】已知数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)若数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求数列
的等比数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,求证:数列
,求证:数列![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
试题(1)易知![]() ,则
,则![]() ,代入
,代入![]() 可得数列
可得数列![]() 的通项公式(2)由
的通项公式(2)由![]() ,则
,则![]() ,可证
,可证![]() 为等差数列,则数列
为等差数列,则数列![]() 的通项公式可求(3)对于给定的
的通项公式可求(3)对于给定的![]() ,若存在
,若存在![]() ,使得
,使得![]() ,
,
只需![]() ,由此能够证明数列
,由此能够证明数列![]() 中的任意一项总可以表示成其他两项之积.
中的任意一项总可以表示成其他两项之积.
试题解析:(1)因为![]() ,
,
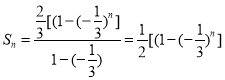 ,
,
所以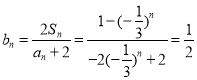 .
.
(2)若![]() ,则
,则![]() ,∴
,∴![]() ,
,
两式相减得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
两式相减得![]() ,即
,即![]() ,
,
又由![]() ,
,![]() 得
得![]() ,
,![]() ,
,
所以数列![]() 是首项为2,公差为3-2=1的等差数列,
是首项为2,公差为3-2=1的等差数列,
故数列![]() 的通项公式是
的通项公式是![]() .
.
(3)由(2)得![]() ,
,
对于给定的![]() ,若存在
,若存在![]() ,使得
,使得![]() ,
,
只需![]() ,
,
即![]() ,即
,即![]() ,则
,则![]() ,
,
取![]() ,则
,则![]() ,
,
∴对数列![]() 中的任意一项
中的任意一项![]() ,都存在
,都存在![]() 和
和![]() 使得
使得![]()

 名校课堂系列答案
名校课堂系列答案【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
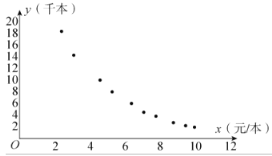
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程设该科普书一个季度的利润总额为![]() (单位:千元),当季销售量
(单位:千元),当季销售量![]() 为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
为何值时,该书一个季度的利润总额预报值最大?(季利润总额=季销售量×每本书的利润)
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.