题目内容
15.已知复数$z=\frac{{{{(1+i)}^2}+2(5-i)}}{3+i}$,(1)求|z|;
(2)若z(z+a)=b+i,求实数a,b的值.
分析 (1)化简复数为a+bi的形式,然后求解复数的模.
(2)利用复数的代数形式的混合运算,结合复数相等,列出方程求解a,b即可.
解答 解:(1)$z=\frac{2i+10-2i}{3+i}=\frac{10}{3+i}=\frac{10(3-i)}{10}=3-i$;$|z|=\sqrt{10}$
(2)(3-i)(3-i+a)=(3-i)2+(3-i)a=8+3a-(a+6)i=b+i,
可得$\left\{\begin{array}{l}8+3a=b\\-(a+6)=1\end{array}\right.⇒\left\{\begin{array}{l}a=-7\\ b=-13\end{array}\right.$.
点评 本题考查复数的代数形式的混合运算,复数相等条件的应用,考查计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.设奇函数f(x)在(-∞,0)上为减函数,且f(2)=0,则$\frac{{f(x)-3f({-x})}}{2x}>0$的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-∞.-2)∪(2.+∞) | D. | (-2,0)∪(0,2) |
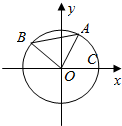 已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α
已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α 已知函数f(x)=x-|x-1|,$g(x)={(\frac{1}{2})^{x-1}}$.
已知函数f(x)=x-|x-1|,$g(x)={(\frac{1}{2})^{x-1}}$.