题目内容
【题目】已知函数y=f(x)的图象与g(x)=logax(a>0,且a≠1)的图象关于x轴对称,且g(x)的图象过(4,2)点.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若f(x﹣1)>f(5﹣x),求x的取值范围.
【答案】解:(Ⅰ)∵g(x)=logax(a>0,且a≠1)的图象过点(4,2),
∴loga4=2,a=2,则g(x)=log2x.
∵函数y=f(x)的图象与g(X)的图象关于x轴对称,
∴ ![]() .
.
(Ⅱ)∵f(x﹣1)>f(5﹣x),
∴ ![]() ,
,
即 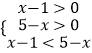 ,解得1<x<3,
,解得1<x<3,
所以x的取值范围为(1,3)
【解析】(Ⅰ)把点(4,2)代入g(x)的解析式求出a,再根据条件求出f(x)的解析式;(Ⅱ)根据(Ⅰ)和对数函数的单调性、真数大于零列出不等式组,求出解集即可.
【考点精析】通过灵活运用对数函数的单调性与特殊点,掌握过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数即可以解答此题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目