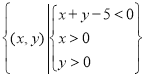题目内容
【题目】（Ⅰ）已知 
是空间的两个单位向量，它们的夹角为60°，设向量 
， 
．求向量 
与 
的夹角； （Ⅱ）已知 
是两个不共线的向量， 
．求证： 
共面．
【答案】解：（Ⅰ）∵ 
是两个单位向量，所以| 
|=| 
|=1，由于其夹角为60° 所以向量 
=cos60°= 
∴ 
=（2 
） 
=﹣6 
+ 
= 
| 
|= 
= 
= 
同理| 
|= ，
所以cos＜ 
＞= 
= 
=-
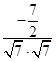所以夹角120°
（Ⅱ） 证明：因为向量 
是两个不共线的向量
设 
=x（ 
）+y（ 
）=（x+3y） 
+（x﹣2y） 
=2 +3
所以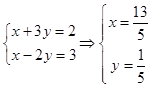 
，
这表明存在实数 
， 
，使 
根据共面向量定理知：向量 
共面
【解析】（Ⅰ）利用向量的夹角公式cos＜ 
＞= 
可求夹角余弦，进而可求夹角（Ⅱ）要证明 
共面，只要证明存在实数x，y，使得 
即可
【考点精析】本题主要考查了平面向量的基本定理及其意义和数量积表示两个向量的夹角的相关知识点，需要掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
；设、
都是非零向量，
，
，
是与
的夹角，则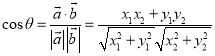
才能正确解答此题．
练习册系列答案
相关题目
