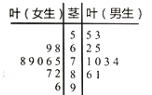
题目内容
【题目】给定方程： 
，则下列命题中：
①该方程没有小于0的实数解；
②该方程有无数个实数解；
③该方程在(－∞，0)内有且只有一个实数解；
④若x0是该方程的实数解，则x0>－1.
正确的命题是________．
【答案】②③④
【解析】试题分析：根据正弦函数的符号和指数函数的性质，可得该方程存在小于0的实数解，故①不正确；根据指数函数的图象与正弦函数的有界性，可得方程有无数个正数解，故②正确；根据y=（
）x﹣1的单调性与正弦函数的有界性，
分析可得当x≤﹣1时方程没有实数解，当﹣1＜x＜0时方程有唯一实数解，由此可得③④都正确．
解：对于①，若α是方程（）x+sinx﹣1=0的一个解，
则满足（）α=1﹣sinα，当α为第三、四象限角时（
）α＞1，
此时α＜0，因此该方程存在小于0的实数解，得①不正确；
对于②，原方程等价于（）x﹣1=﹣sinx，
当x≥0时，﹣1＜（）x﹣1≤0，而函数y=﹣sinx的最小值为﹣1
且用无穷多个x满足﹣sinx=﹣1，
因此函数y=（）x﹣1与y=﹣sinx的图象在[0，+∞）上有无穷多个交点
因此方程（）x+sinx﹣1=0有无数个实数解，故②正确；
对于③，当x＜0时，
由于x≤﹣1时（）x﹣1≥1，函数y=（）x﹣1与y=﹣sinx的图象不可能有交点
当﹣1＜x＜0时，存在唯一的x满足（）x=1﹣sinx，
因此该方程在（﹣∞，0）内有且只有一个实数解，得③正确；
对于④，由上面的分析知，
当x≤﹣1时（）x﹣1≥1，而﹣sinx≤1且x=﹣1不是方程的解
∴函数y=（）x﹣1与y=﹣sinx的图象在（﹣∞，﹣1]上不可能有交点
因此只要x0是该方程的实数解，则x0＞﹣1．
故答案为：②③④
练习册系列答案
相关题目
