题目内容
过椭圆
(
)的左焦点
作
轴的垂线交椭圆于点
，
为右焦点，若
，则椭圆的离心率为( )
()的左焦点作轴的垂线交椭圆于点，为右焦点，若，则椭圆的离心率为( )A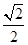． | B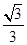． | C． | D． |
B
此题考查椭圆的性质的应用、离心率的求法；由已 知可得出：
，在
中，
，选B
，在中，，选B
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
()的左焦点作轴的垂线交椭圆于点，为右焦点，若，则椭圆的离心率为( )| A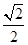． | B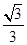． | C． | D． |
，在中，，选B阅读快车系列答案
＋
＝1
的左．右焦点为
，离心率为
，直线
与x轴、y轴分别交于点
，
是直线
与椭圆C的一个公共点，
是点
关于直线
＝
； （Ⅱ）确定
的值，使得
是等腰三角形.
分别是椭圆： 
(
)的左、右焦点，过
斜率为1的直线
与该椭圆相交于P，Q两点，且
，
，
成等差数列．
的中心在坐标原点，焦点在
轴上,离心率为
,椭圆的短轴端点和焦点所组成的四边形周长等于8。
的直线
与椭圆
两点(
不是左右顶点),且以
为直径的圆过椭圆
有公共的焦点，则双曲线C的方程为____________。
的左右焦点是F1，F2，设P是双曲线右支上一点，
在
上的投影的大小恰好为｜
，则双曲线的离心率e为
中,
为椭圆上的一点，过坐标原点
的直线交椭圆于
两点，其中
在第一象限，过
轴的垂线，垂足为
,连接
,
与
的斜率均存在，问它们的斜率之积是否为定值，若是，求出这个定值，若不是，说明理由；
的延长线与椭圆的交点，求证：
.
＝1的右焦点重合，该抛物线上有一点M，它在y轴上的射影为N，则|MA|＋|MN|的最小值为___________。
的一个焦点坐标为(0,1)，则实数
的值等于_____ ____,