题目内容
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆的短轴端点和焦点所组成的四边形周长等于8。
,椭圆的短轴端点和焦点所组成的四边形周长等于8。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点(
两点(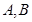 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求直线
的右顶点,求直线 的方程。
的方程。
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆的短轴端点和焦点所组成的四边形周长等于8。
,椭圆的短轴端点和焦点所组成的四边形周长等于8。(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点(
两点(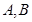 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求直线
的右顶点,求直线 的方程。
的方程。解:(Ⅰ)由题意设椭圆的标准方程为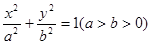
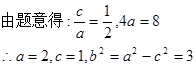 ∴椭圆的标准方程为
∴椭圆的标准方程为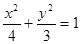
(Ⅱ)当直线l与x轴垂直时,A,B分别为椭圆短轴的两端点,显然以A,B为直径的圆不过椭圆C的右顶点,故直线l与x轴不垂直
设直线l的方程为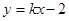
则由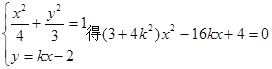
由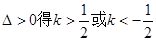
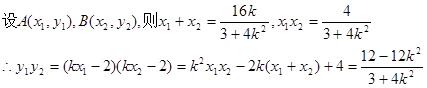
因为以AB为直径的圆过椭圆C的右顶点D(2,0),

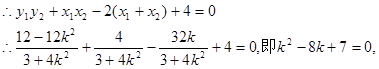
解得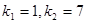
当k=1时,直线l过椭圆右顶点(2,0),不合题意,
所以k=7,故直线l的方程是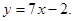
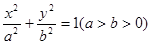
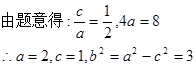 ∴椭圆的标准方程为
∴椭圆的标准方程为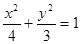
(Ⅱ)当直线l与x轴垂直时,A,B分别为椭圆短轴的两端点,显然以A,B为直径的圆不过椭圆C的右顶点,故直线l与x轴不垂直
设直线l的方程为
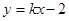
则由
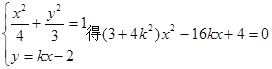
由
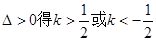
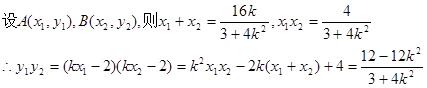
因为以AB为直径的圆过椭圆C的右顶点D(2,0),

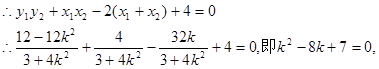
解得
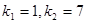
当k=1时,直线l过椭圆右顶点(2,0),不合题意,
所以k=7,故直线l的方程是
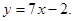
略

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
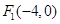 ,
,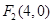 ,P在椭圆上,若 △
,P在椭圆上,若 △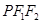 的面积的最大值为12,则椭圆方程为
的面积的最大值为12,则椭圆方程为



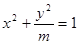 的下焦点为
的下焦点为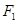 、上焦点为
、上焦点为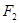 ,其离心 率
,其离心 率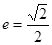 。过焦点F2且与
。过焦点F2且与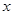 轴不垂直的直线l交椭圆于A、B两点。
轴不垂直的直线l交椭圆于A、B两点。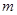 的值;
的值;  与椭圆
与椭圆 交于A、B两点,点F为抛物线
交于A、B两点,点F为抛物线 ,则椭圆的离心率为
,则椭圆的离心率为  B、
B、 C、
C、 D、
D、
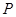 是椭圆
是椭圆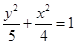 上的一点,
上的一点,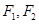 是焦点,且
是焦点,且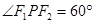 ,则
,则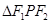 的面积为
的面积为  (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )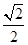
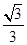


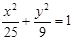 上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若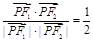 ,则
,则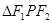 的面积为( )
的面积为( )

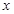 轴上,离心率
轴上,离心率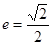 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为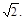
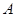 为椭圆左顶点,
为椭圆左顶点,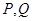 为椭圆上异于
为椭圆上异于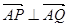 ,求证:直线
,求证:直线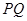 过定点并求出定点坐标。
过定点并求出定点坐标。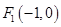 和
和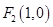 ,点
,点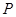 在椭圆上的一点,且
在椭圆上的一点,且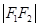 是
是 的等差中项,则该椭圆的方程为( )
的等差中项,则该椭圆的方程为( )


