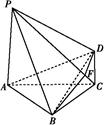
题目内容
已知多面体 中, 四边形
中, 四边形 为矩形,
为矩形,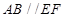 ,
,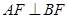 ,平面
,平面 平面
平面 ,
,  、
、 分别为
分别为 、
、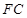 的中点,且
的中点,且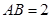 ,
,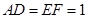 .
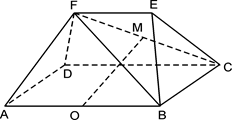
.
(1)求证: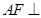 平面
平面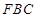 ;
;
(2)求证: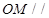 平面
平面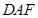 ;
;
(3)设平面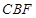 将几何体
将几何体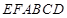 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为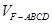 ,
,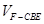 ,求
,求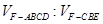 的值.
的值.
(1)见解析;(2)见解析;(3)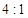 .
.
解析试题分析:(1)通过证明 ⊥
⊥ ,
, ⊥
⊥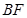 即可证明
即可证明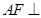 平面
平面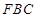 ;
;
(2)取 中点
中点 ,证明
,证明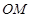
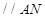 即可证明
即可证明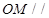 平面
平面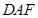 ;
;
(3)将两个几何体的体积分别用相同的量表示出,然后作比即可.
试题解析:(1)∵平面 ⊥平面
⊥平面 ,平面
,平面 平面
平面 ,
,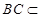 平面
平面 ,四边形
,四边形 为矩形,
为矩形,
∴ ⊥
⊥ ,∴
,∴ ⊥平面
⊥平面 .
.
∵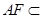 平面
平面 ,∴
,∴ ⊥
⊥ ,
,
∵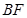 ⊥
⊥ ,
, ,∴
,∴ ⊥平面
⊥平面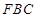 .
.
(2)取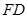 中点
中点 ,连结
,连结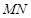 、
、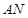 ,则
,则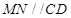 ,且
,且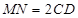 ,
,
又四边形 为矩形,
为矩形,
∴ ,且
,且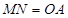 ,
,
∴四边形 为平行四边形,∴
为平行四边形,∴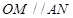 ,
,
又∵ 平面
平面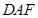 ,
,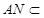 平面
平面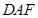 ,
,
∴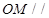 平面
平面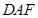 .
.
(3)过 作
作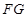 ⊥
⊥ 于
于 ,由题意可得
,由题意可得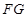 ⊥平面
⊥平面 ,
,
∴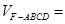
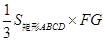
 .
.
∵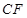 ⊥平面
⊥平面 ,
,
∴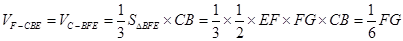 ,
,
∴ .
.
考点:1.几何体中线面的平行、垂直证明;2.几何体的体积计算.

练习册系列答案
相关题目
 中,底面
中,底面 为正方形,
为正方形,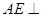 平面
平面 ,已知
,已知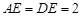 ,
,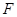 为线段
为线段 的中点.
的中点.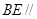 平面
平面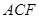 ;
;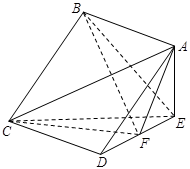
 与
与 都是边长为
都是边长为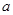 的正方形,点
的正方形,点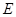 是
是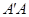 的中点,
的中点,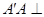 平面
平面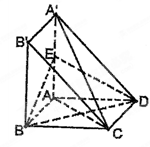
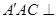 平面
平面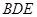 ;
; 的体积.
的体积.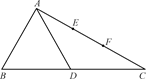

 ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=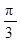 .
.
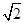 .
.
 A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=
A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=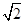 .
.

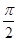 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。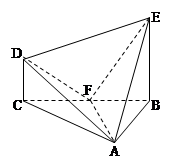
 ,求证:
,求证: