题目内容
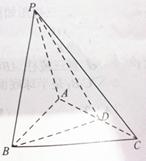
在几何体ABCDE中,∠BAC=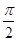 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。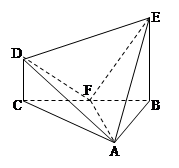
(1)设平面ABE与平面ACD的交线为直线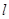 ,求证:
,求证: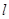 ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积。
(1)详见解析;(2)详见解析;(3)V=2.
解析试题分析: (1) 由DC⊥平面ABC,EB⊥平面ABC可得DC//EB,从而DC∥平面ABE.再由线面平行的性质定理可得DC∥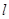 ,又由线面平行的判定定理可得
,又由线面平行的判定定理可得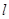 ∥平面BCDE;(2)证面面垂直,首先考虑证哪条线垂直哪个面. 结合题设和图形,可考虑证FD⊥平面AFE.因为在△DEF中,由所给长度及勾股定理可得EF⊥FD.由DC⊥平面ABC可得DC⊥AF,又由AB=AC,F是BC的中点,可得AF⊥BC,从而AF⊥平面BCDE,AF⊥FD.这样由EF⊥FD,AF⊥FD可得FD⊥平面AFE,从而得平面AFD⊥平面AFE.(3)该几何体是一个四棱锥,其顶点为A,底面为BCDE.
∥平面BCDE;(2)证面面垂直,首先考虑证哪条线垂直哪个面. 结合题设和图形,可考虑证FD⊥平面AFE.因为在△DEF中,由所给长度及勾股定理可得EF⊥FD.由DC⊥平面ABC可得DC⊥AF,又由AB=AC,F是BC的中点,可得AF⊥BC,从而AF⊥平面BCDE,AF⊥FD.这样由EF⊥FD,AF⊥FD可得FD⊥平面AFE,从而得平面AFD⊥平面AFE.(3)该几何体是一个四棱锥,其顶点为A,底面为BCDE.
试题解析:(1) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,又∵DC 平面ABE,EB
平面ABE,EB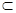 平面ABE,
平面ABE,
∴DC∥平面ABE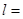 平面ABE
平面ABE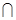 平面ACD,则DC∥
平面ACD,则DC∥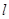
又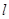
 平面BCDE,CD
平面BCDE,CD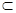 平面BCDE
平面BCDE
所以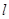 ∥平面BCDE. 4分
∥平面BCDE. 4分
(2)在△DEF中,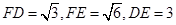 ,由勾股定理知,
,由勾股定理知,
由DC⊥平面ABC,AF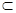 平面ABC,∴DC⊥AF,
平面ABC,∴DC⊥AF,
又∵AB=AC,F是BC的中点,∴AF⊥BC,
又∵DC∩BC=C,DC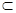 平面BCDE ,BC
平面BCDE ,BC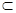 平面BCDE,
平面BCDE,
∴AF⊥平面BCDE,∴AF⊥FD,又∵AF∩FE=F,∴FD⊥平面AFE,
又FD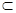 平面AFD,故平面AFD⊥平面AFE. 9分
平面AFD,故平面AFD⊥平面AFE. 9分
(3)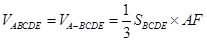 =
=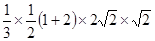 =2. 12分
=2. 12分
考点:1、空间直线与平面的关系;2、几何体的体积.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 中, 四边形
中, 四边形 为矩形,
为矩形,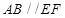 ,
,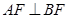 ,平面
,平面 平面
平面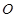 、
、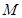 分别为
分别为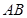 、
、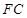 的中点,且
的中点,且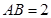 ,
,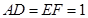 .
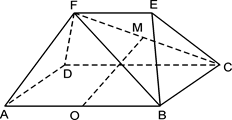
.
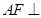 平面
平面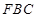 ;
;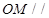 平面
平面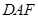 ;
; 将几何体
将几何体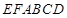 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为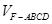 ,
,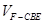 ,求
,求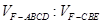 的值.
的值.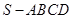 中,
中,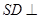 底面
底面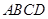 ,底面
,底面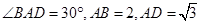 ,
,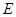 是
是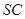 的中点。
的中点。
 ;
; 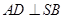 ;
;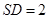 ,求二面角
,求二面角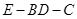 的余弦值.
的余弦值.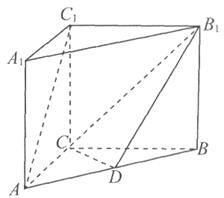
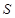 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
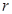 表示出储油灌的容积
表示出储油灌的容积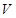 ,并写出
,并写出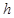 与半径
与半径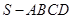 中,底面
中,底面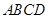 是正方形,
是正方形,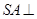 底面
底面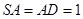 ,点
,点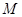 是
是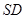 的中点,
的中点,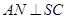 ,交
,交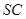 于点
于点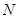 .
.
 平面
平面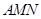 ;
;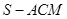 的体积.
的体积.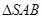 ,
,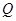 为底面圆周上一点.
为底面圆周上一点.
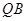 的中点为
的中点为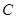 ,
,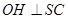 ,
,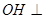 平面
平面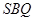 ;
;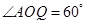 ,
,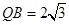 ,求此圆锥的全面积.
,求此圆锥的全面积.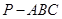 中,
中, ,
,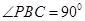 ,D为AC的中点,
,D为AC的中点, .
.
 平面
平面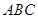 ;
;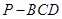 的体积为3,求
的体积为3,求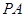 .
.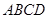 与直角梯形
与直角梯形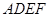 所在平面互相垂直,
所在平面互相垂直, ,
,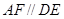 ,
, .
.
 平面
平面 ;
; 的体积.
的体积.