题目内容
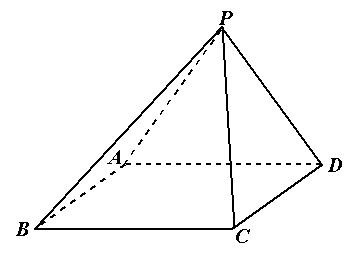
如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2
ABCD中,PA⊥底面ABCD,PA=2 ,BC="CD=2," ∠ACB=∠ACD=
,BC="CD=2," ∠ACB=∠ACD=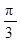 .
.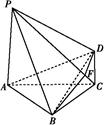
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.
BDF的体积.
(1)见解析 (2) 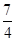
解析(1)证明:因为BC=CD,所以△BCD为等腰三角形,
又∠ACB=∠ACD,故BD⊥AC.
因为PA⊥底面ABCD,所以PA⊥BD.
从而BD与平面PAC内两条相交直线PA,AC都垂直,
所以BD⊥平面PAC.
(2)解:三棱锥P BCD的底面BCD的面积S△BCD=
BCD的底面BCD的面积S△BCD=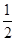 BC·CD·sin∠BCD=
BC·CD·sin∠BCD=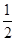 ×2×2×sin
×2×2×sin 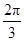 =
= .
.
由PA⊥底面ABCD,得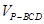 =
=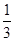 ·S△BCD·PA=
·S△BCD·PA=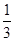 ×
× ×2
×2 =2.
=2.
由PF=7FC,得三棱锥F BCD的高为
BCD的高为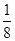 PA,
PA,
故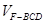 =
=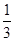 ·S△BCD·
·S△BCD·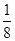 PA=
PA=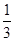 ×
× ×
×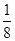 ×2
×2 =
=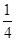 ,
,
所以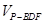 =
=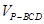 -
-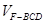 =2-
=2-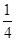 =
=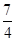 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
一个空间几何体的三视图如下左图所示,则该几何体的表面积为( )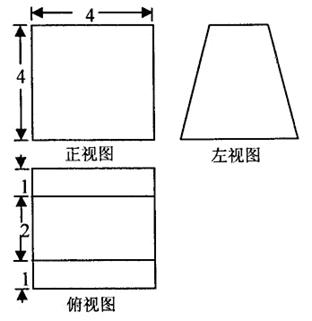
| A.48 | B.48+8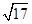 | C.32+8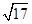 | D.80 |
 的边长为
的边长为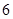 ,点
,点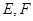 分别在边
分别在边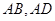 上,
上,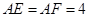 ,现将△
,现将△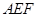 沿线段
沿线段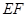 折起到△
折起到△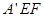 位置,使得
位置,使得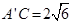 .
.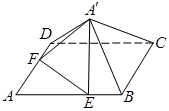
 的体积;
的体积;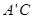 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面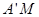 ;若不存在,说明理由.
;若不存在,说明理由. .
.
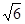 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积. 中, 四边形
中, 四边形 为矩形,
为矩形,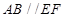 ,
,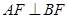 ,平面
,平面 平面
平面 、
、 分别为
分别为 、
、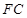 的中点,且
的中点,且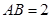 ,
,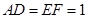 .
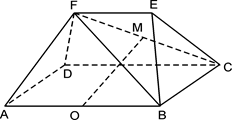
.
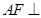 平面
平面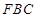 ;
;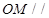 平面
平面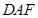 ;
;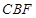 将几何体
将几何体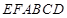 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为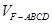 ,
,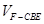 ,求
,求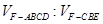 的值.
的值. ,AB=2CD=8.
,AB=2CD=8.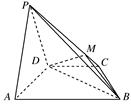
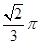 的圆锥
的圆锥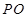 中,已知
中,已知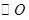 的直径
的直径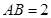 ,
, 是
是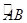 的中点,
的中点,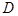 是弦
是弦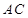 的中点.
的中点.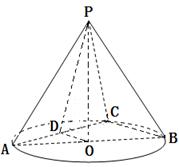
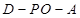 的平面角,并求出它的大小;
的平面角,并求出它的大小;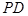 与
与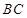 所成的角的正切值.
所成的角的正切值.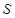 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.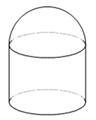
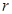 表示出储油灌的容积
表示出储油灌的容积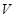 ,并写出
,并写出 与半径
与半径