题目内容
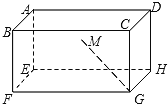
【题目】如图所示,在长方体![]() 中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为
中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为![]() 那么点M到平面EFGH的距离是_____.
那么点M到平面EFGH的距离是_____.
【答案】![]()
【解析】
取FG的中点N,作MO⊥EH于O,连接MN,ON,MH,OG,通过MG和平面EFGH所成角的正切值为![]() ,推出
,推出![]() ,然后求解即可.
,然后求解即可.
解:取FG的中点N,作MO⊥EH于O,连接MN,ON,MH,OG,
在长方体ABCD﹣A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,可得△MNG≌△MGH,则△ONG≌△OGH,
所以ON=GH=AB=1,
因为N是FG的中点,所以NG![]() FG
FG![]() AD
AD![]() 2=1,
2=1,
所以在Rt△ONG中,OG![]()
MG和平面EFGH所成角的正切值为![]() ,可得
,可得
![]() ,则MO
,则MO![]() .
.
则点M到平面EFGH的距离为:![]() .
.
故答案为:![]() .
.


练习册系列答案
相关题目
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记![]() 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.