题目内容
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点O,数列
,且过坐标原点O,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() (
(![]() )在二次函数
)在二次函数![]() 的图象上.
的图象上.
(1)求数列![]() 的表达式;
的表达式;
(2)设![]() (
(![]() ),数列
),数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)在数列![]() 中是否存在这样的一些项,
中是否存在这样的一些项,![]() ,
,![]() ,
,![]() ,…
,…![]() ,…(
,…(![]() ),这些项能够依次构成以
),这些项能够依次构成以![]() 为首项,q(
为首项,q(![]() ,
,![]() )为公比的等比数列
)为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于k的表达式;若不存在,说明理由.
关于k的表达式;若不存在,说明理由.
【答案】(1) ![]() (
(![]() ) (2)见解析 (3) 存在,
) (2)见解析 (3) 存在,![]() ,(
,(![]() ).
).
【解析】
(1)先求出![]() ,通过讨论n的范围,从而得到数列
,通过讨论n的范围,从而得到数列![]() 的通项公式;
的通项公式;
(2)通过讨论n的奇偶性,从而求出![]() 的表达式,问题转化为使
的表达式,问题转化为使![]() (n为正偶数)恒成立即可;
(n为正偶数)恒成立即可;
(3)通过讨论公比的奇偶性,从而得到答案.
(1)由题意得![]() ,
,
∴![]() (
(![]() ),
),
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 适合上式,
适合上式,
∴数列![]() 的通项公式是:
的通项公式是:![]() (
(![]() );
);
(2)∵![]() ,(
,(![]() ),
),
∴![]()
![]() ,
,
由(1)得:数列![]() 是以1为首项,公差为
是以1为首项,公差为![]() 的等差数列,
的等差数列,
①当![]() ,
,![]() 时,
时,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
②当![]() ,
,![]() 时,
时,
![]()
![]()
![]()
![]() ,
,
∴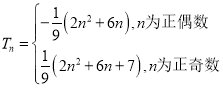 ,要使
,要使![]() 对
对![]() 恒成立,
恒成立,
只要使![]() (n为正偶数)恒成立,
(n为正偶数)恒成立,
即使![]() 对n为正偶数恒成立.
对n为正偶数恒成立.
∴![]() ;
;
(3)由![]() 知,数列
知,数列![]() 中每一项都不可能是偶数,
中每一项都不可能是偶数,
①如存在以![]() 为首项,公比q为2或4的数列
为首项,公比q为2或4的数列![]() ,
,![]() ,此时
,此时![]() 中每一项除第一项外都是偶数,
中每一项除第一项外都是偶数,
故不存在以![]() 为首项,公比为偶数的数列
为首项,公比为偶数的数列![]() ;
;
②![]() 时,显然不存在这样的数列
时,显然不存在这样的数列![]() ,
,
![]() 时,若存在以
时,若存在以![]() 为首项,公比为3的数列
为首项,公比为3的数列![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴存在满足条件的数列![]() ,且
,且![]() ,(
,(![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
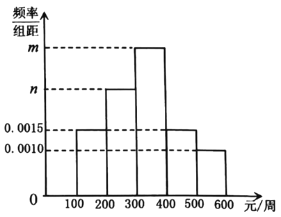
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()