Question

【题目】已知二次函数和.

（1）为偶函数，试判断的奇偶性；

（2）若方程有两个不相等的实根，当时判断在上的单调性；

（3）当时，问是否存在x的值，使满足且的任意实数a，不等式恒成立？并说明理由.

Answer 1

【答案】（1）为奇函数（2）答案不唯一，具体见解析（3）存在，详见解析

【解析】

（1）根据偶函数的定义可知，可求出的值，求出的定义域看是否对称，然后根据奇偶性定义进行判定；

（2）有两个不相等的实根可转化成，可判定对称轴的范围，从而确定函数在上的单调性；

（3）不等式恒成立可转化成对于且时恒成立，建立不等式组，解之即可求出所求.

解：（1）若为偶函数，有，则，定义域为，且，所以为奇函数.

（2）由，整理得：，且，即或，又的对称轴为

所以当时，在上为增函数；当时，在上为减函数.

（3）由，即，有

由已知它对于且时上面不等式恒成立，则有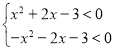

解得：.