题目内容
6.定义一种运算如下:$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$=ad-bc,则复数$[\begin{array}{l}{1-i}&{-1}\\{2}&{3i}\end{array}]$的共轭复数是5-3i.分析 由新定义和复数的运算可化简式中的复数,可得其共轭复数.
解答 解:由题意可得$[\begin{array}{l}{1-i}&{-1}\\{2}&{3i}\end{array}]$
=(1-i)•3i-(-1)•2
=3i-3i2+2=5+3i,
∴共轭复数为:5-3i,
故答案为:5-3i
点评 本题考查复数的代数形式的混合运算,属基础题.

练习册系列答案
相关题目
1.已知a、b为异面直线,若c∥a,则c与b的位置关系是( )
| A. | 相交 | B. | 异面 | C. | 平行 | D. | 相交或异面. |
18.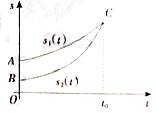 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )| A. | v甲>v乙 | B. | v甲<v乙 | C. | v甲=v乙 | D. | 大小关系不确定 |

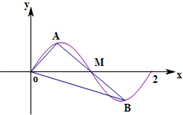 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )