题目内容
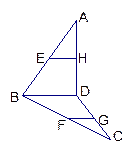
两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证: MN∥平面BCE。
证明略
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB.
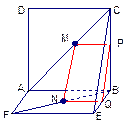 ∴MP∥NQ,又AM=NF,AC=BF,
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ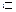 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE
证法二: 如图过M作MH⊥AB于H,则MH∥BC,
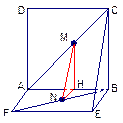
∴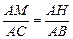
连结NH,由BF=AC,FN=AM,得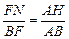
∴ NH//AF//BE
由MH//BC, NH//BE得:平面MNH//平面BCE
∴MN∥平面BCE.
 ∴MP∥NQ,又AM=NF,AC=BF,
∴MP∥NQ,又AM=NF,AC=BF,∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ
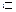 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,∴MN∥平面BCE

证法二: 如图过M作MH⊥AB于H,则MH∥BC,

∴
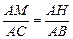
连结NH,由BF=AC,FN=AM,得
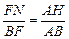
∴ NH//AF//BE
由MH//BC, NH//BE得:平面MNH//平面BCE
∴MN∥平面BCE.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
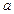 、
、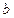 ,
,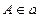 ,
,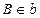 ,
,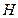 为
为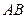 中点,
中点,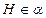 ,
,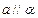 ,
,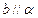 ,
,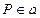 ,
,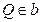 ,
,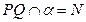 ,求:
,求: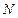 为
为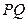 中点。
中点。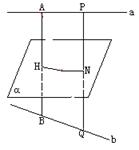
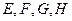 为空间四边形
为空间四边形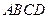 的边
的边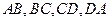 上的点,且
上的点,且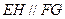 .求证:
.求证: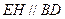 .
. 
 平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC
平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC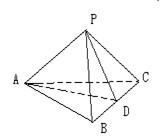
 a∥b;②a∥c,b∥c
a∥b;②a∥c,b∥c