题目内容
已知函数 (其中
(其中 ).
).
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)求 在
在 上的最大值与最小值.
上的最大值与最小值.
 (其中
(其中 ).
).(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)求
 在
在 上的最大值与最小值.
上的最大值与最小值.(Ⅰ) 的单调递增区间是
的单调递增区间是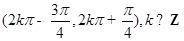 ,单调递减区间是
,单调递减区间是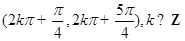 .
.
(Ⅱ)当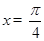 时,
时, 在
在 上取得最大值
上取得最大值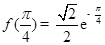 ;当
;当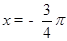 时,
时, 在
在 上取得最小值
上取得最小值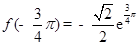 .
.
 的单调递增区间是
的单调递增区间是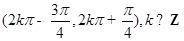 ,单调递减区间是
,单调递减区间是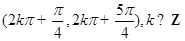 .
.(Ⅱ)当
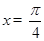 时,
时, 在
在 上取得最大值
上取得最大值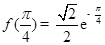 ;当
;当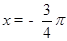 时,
时, 在
在 上取得最小值
上取得最小值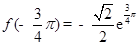 .
.(I)直接求导利用导数大(小)于零,求其单调增(减)区间即可.
(II)在(I)的基础上可确定函数 在
在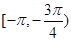 上单调递减,在
上单调递减,在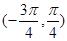 上单调递增,在
上单调递增,在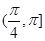 上单调递减.然后分别求出其极值和区间的端点值,进行比较找出函数在特定区间上的最大值和最小值
上单调递减.然后分别求出其极值和区间的端点值,进行比较找出函数在特定区间上的最大值和最小值
(Ⅰ)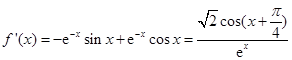 .
.
令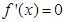 ,解得:
,解得: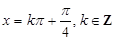 .
.
因为当 时,
时,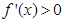 ;
;
当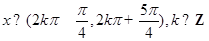 时,
时,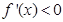 ,
,
所以 的单调递增区间是
的单调递增区间是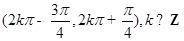 ,单调递减区间是
,单调递减区间是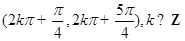 .
.
(Ⅱ)由(Ⅰ)知, 在
在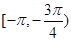 上单调递减,在
上单调递减,在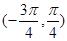 上单调递增,在
上单调递增,在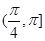 上单调递减.
上单调递减. 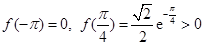 ,
, 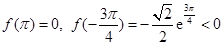
所以 在
在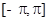 上的最大值为
上的最大值为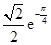 ,最小值为
,最小值为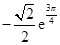 .
.
当 时,
时,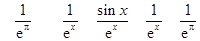 .因为
.因为 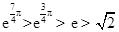 ,
,
所以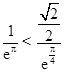 ,即
,即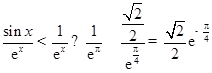 ,
,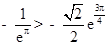 ,即
,即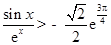 .
.
综上所述,当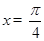 时,
时, 在
在 上取得最大值
上取得最大值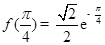 ;当
;当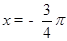 时,
时, 在
在 上取得最小值
上取得最小值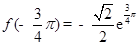 .
.
(II)在(I)的基础上可确定函数
 在
在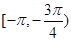 上单调递减,在
上单调递减,在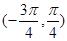 上单调递增,在
上单调递增,在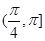 上单调递减.然后分别求出其极值和区间的端点值,进行比较找出函数在特定区间上的最大值和最小值
上单调递减.然后分别求出其极值和区间的端点值,进行比较找出函数在特定区间上的最大值和最小值(Ⅰ)
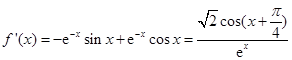 .
.令
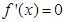 ,解得:
,解得: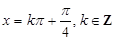 .
.因为当
 时,
时,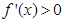 ;
;当
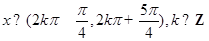 时,
时,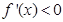 ,
,所以
 的单调递增区间是
的单调递增区间是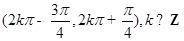 ,单调递减区间是
,单调递减区间是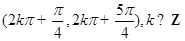 .
.(Ⅱ)由(Ⅰ)知,
 在
在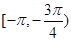 上单调递减,在
上单调递减,在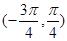 上单调递增,在
上单调递增,在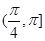 上单调递减.
上单调递减. 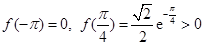 ,
, 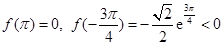
所以
 在
在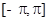 上的最大值为
上的最大值为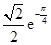 ,最小值为
,最小值为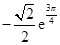 .
.当
 时,
时,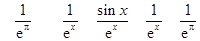 .因为
.因为 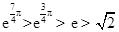 ,
,所以
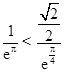 ,即
,即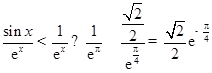 ,
,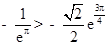 ,即
,即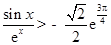 .
.综上所述,当
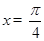 时,
时, 在
在 上取得最大值
上取得最大值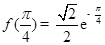 ;当
;当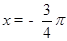 时,
时, 在
在 上取得最小值
上取得最小值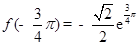 .
.
练习册系列答案
相关题目
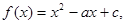 (其中
(其中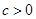 )
) 的奇偶性.
的奇偶性.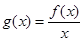 ,
,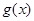 在
在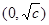 上单调递减,在
上单调递减,在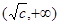 上单调递增;
上单调递增; 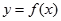 ,则
,则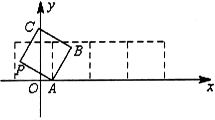
 有两个不相等的实根,则实数
有两个不相等的实根,则实数 的取值范围是 ( )
的取值范围是 ( )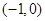



 上的函数
上的函数 满足
满足 ,且当
,且当 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内零点个数是( )
内零点个数是( ) .
.
 .
.
 .
.
 .
.
 的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/
的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/ , 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元? 的不等式
的不等式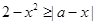 至少有一个负数解,则
至少有一个负数解,则 的最小值为_______.
的最小值为_______. 的图象总在
的图象总在 轴的上方,则实数
轴的上方,则实数 的取值范围是
的取值范围是


 .
. 的方程组
的方程组 有唯一的一组实数解,则实数
有唯一的一组实数解,则实数 的值为_____________.
的值为_____________.