题目内容
已知二次函数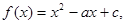 (其中
(其中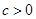 )
)
(1)试讨论函数 的奇偶性.
的奇偶性.
(2)当 为偶函数时,若函数
为偶函数时,若函数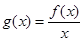 ,
,
试证明:函数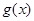 在
在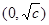 上单调递减,在
上单调递减,在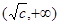 上单调递增;
上单调递增;
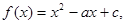 (其中
(其中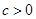 )
)(1)试讨论函数
 的奇偶性.
的奇偶性.(2)当
 为偶函数时,若函数
为偶函数时,若函数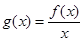 ,
,试证明:函数
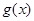 在
在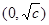 上单调递减,在
上单调递减,在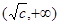 上单调递增;
上单调递增; (1)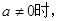 函数
函数 是非奇非偶函数
是非奇非偶函数
(2)见解析
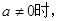 函数
函数 是非奇非偶函数
是非奇非偶函数(2)见解析
本试题主要是考查了二次函数的性质,以及函数奇偶性和单调性的综合运用。
(1)函数 的定义域为R关于原点对称,………
的定义域为R关于原点对称,……… 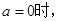
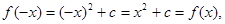 故此时函数
故此时函数 是偶函数
是偶函数
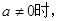
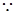
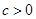 ,
,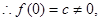 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时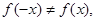 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以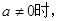 函数
函数 是非奇非偶函数
是非奇非偶函数
(2)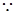
 为偶函数,由(1)知
为偶函数,由(1)知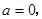
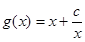 利用定义法判定单调性。
利用定义法判定单调性。
解:(1) 函数 的定义域为R关于原点对称,………. 1分
的定义域为R关于原点对称,………. 1分
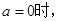
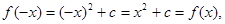 故此时函数
故此时函数 是偶函数……….2分
是偶函数……….2分
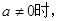
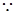
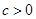 ,
,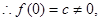 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时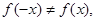 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以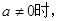 函数
函数 是非奇非偶函数……….4分
是非奇非偶函数……….4分
(其他合理方式解答相应给分)
(2)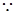
 为偶函数,由(1)知
为偶函数,由(1)知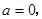
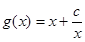 ……….5分
……….5分
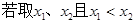 ,则
,则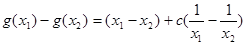 ……….7分
……….7分
=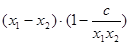
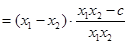 ……………9分
……………9分
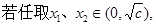
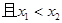 ,则
,则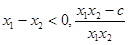 <0
<0
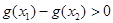 ,
, 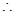
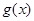 在
在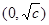 上单调递减, ……….11分
上单调递减, ……….11分
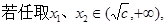
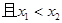 ,则
,则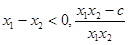 >0
>0
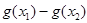 <0 ,
<0 , 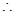
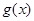 在
在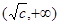 上单调递增, ……….13分
上单调递增, ……….13分
(1)函数
 的定义域为R关于原点对称,………
的定义域为R关于原点对称,……… 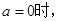
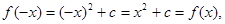 故此时函数
故此时函数 是偶函数
是偶函数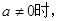
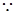
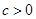 ,
,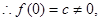 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时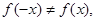 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以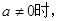 函数
函数 是非奇非偶函数
是非奇非偶函数(2)
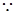
 为偶函数,由(1)知
为偶函数,由(1)知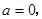
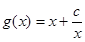 利用定义法判定单调性。
利用定义法判定单调性。解:(1) 函数
 的定义域为R关于原点对称,………. 1分
的定义域为R关于原点对称,………. 1分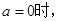
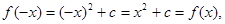 故此时函数
故此时函数 是偶函数……….2分
是偶函数……….2分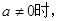
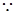
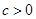 ,
,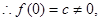 故函数
故函数 不是奇函数,且易知此时
不是奇函数,且易知此时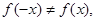 故函数
故函数 也不是偶函数,所以
也不是偶函数,所以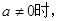 函数
函数 是非奇非偶函数……….4分
是非奇非偶函数……….4分(其他合理方式解答相应给分)
(2)
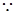
 为偶函数,由(1)知
为偶函数,由(1)知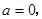
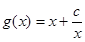 ……….5分
……….5分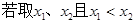 ,则
,则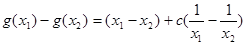 ……….7分
……….7分=
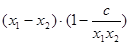
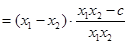 ……………9分
……………9分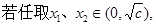
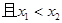 ,则
,则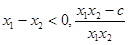 <0
<0 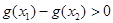 ,
, 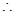
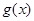 在
在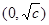 上单调递减, ……….11分
上单调递减, ……….11分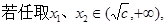
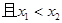 ,则
,则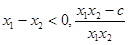 >0
>0 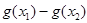 <0 ,
<0 , 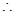
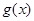 在
在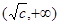 上单调递增, ……….13分
上单调递增, ……….13分
练习册系列答案
相关题目
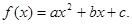
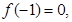 试判断函数
试判断函数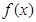 零点个数;
零点个数;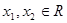 ,且
,且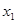 <
<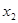 ,
,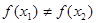 (
(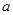 >0),试证明:
>0),试证明: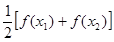 >
>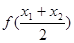 成立。
成立。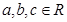 ,使
,使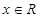 ,
,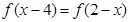 ,且
,且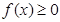 ②对任意的
②对任意的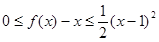 ?若存在,求出
?若存在,求出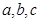 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
 且
且 的图象上存在不同两点
的图象上存在不同两点 ,且
,且 的取值范围是
的取值范围是 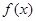 在
在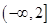 为增函数,且
为增函数,且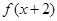 是
是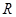 上的偶函数,若
上的偶函数,若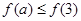 ,则实数
,则实数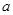 的取值范围是
的取值范围是 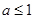
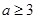
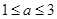
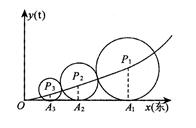
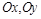 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点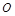 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线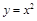 的一段,在小道上依次以点
的一段,在小道上依次以点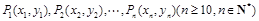 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道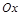 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若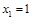 (单位:百米)且
(单位:百米)且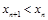 .
.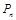 为圆心的圆与主干道
为圆心的圆与主干道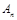 点,证明:数列
点,证明:数列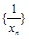 是等差数列,并求
是等差数列,并求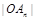 关于
关于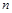 的表达式;
的表达式;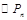 的面积为
的面积为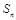 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为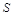 的圆型小道的施工工时为
的圆型小道的施工工时为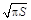 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 (其中
(其中 ).
). 的单调区间;
的单调区间; 上的最大值与最小值.
上的最大值与最小值.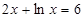 的解为
的解为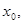 则
则 所在的区间是( )
所在的区间是( )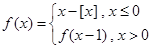 ,其中
,其中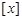 表示不超过
表示不超过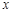 的最大整数,如:
的最大整数,如: 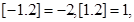
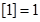 . 则(i)
. 则(i) ;
;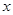 的方程
的方程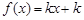 有三个不同的根,则实数
有三个不同的根,则实数 的取值范围是.
的取值范围是.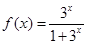 (
(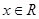 ),正项等比数列
),正项等比数列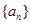 满足
满足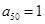 ,则
,则